A B. 5421. feladat (2024. november)

B. 5421. A hegyesszögű $\displaystyle ABC$ háromszög beírt körének középpontja $\displaystyle I$, sugara $\displaystyle r$, a $\displaystyle BC$ oldalhoz írt körének középpontja $\displaystyle I_a$, sugara $\displaystyle r_a$, továbbá a körülírt körének sugara $\displaystyle R$. Az $\displaystyle II_a$ szakasz hossza $\displaystyle r_a+R-r$. Igazoljuk, hogy $\displaystyle BAC\sphericalangle=60^\circ$.

Budapesti Fazekas M. Gyak. Ált. Isk. és Gimn., 2024C.

(6 pont)

A beküldési határidő 2024. december 10-én LEJÁRT.

Megoldás. A feladat szövegében szereplő jelöléseken kívül legyen a háromszög $\displaystyle A$ csúcsánál fekvő szög $\displaystyle \alpha$, $\displaystyle M$ a háromszög magasságpontja, továbbá $\displaystyle F$ a Feuerbach-kör középpontja.

A megoldás során több ismert tényt fogunk bizonyítás nélkül felhasználni:

1. A Feurbach-kör sugara $\displaystyle \frac R2$.

2. A Feuerbach-kör $\displaystyle F$ középpontja az $\displaystyle OM$ szakasz felezőpontja.

3. A magasságpont és az $\displaystyle A$ csúcs távolsága: $\displaystyle MA=2R\cos\alpha$.

4. A hozzáírt körök kívülről érintik a Feuerbach-kört, a beírt kör pedig belülről. A tétel két bizonyítását is olvashatjuk Füredi Zoltán KöMaL cikkében.

Először azt mutatjuk meg, hogy az $\displaystyle A$-ból induló magasság egyenese és az $\displaystyle A$ csúcsot a körülírt kör $\displaystyle O$ középpontjával összekötő sugár egyenese egymás tükörképei az $\displaystyle A$-hoz tartozó belső szögfelezőre.

Legyen az ábra szerint az $\displaystyle A$-hoz tartozó magasság talppontja $\displaystyle T$, az $\displaystyle AC$ oldal felezőpontja $\displaystyle E$.

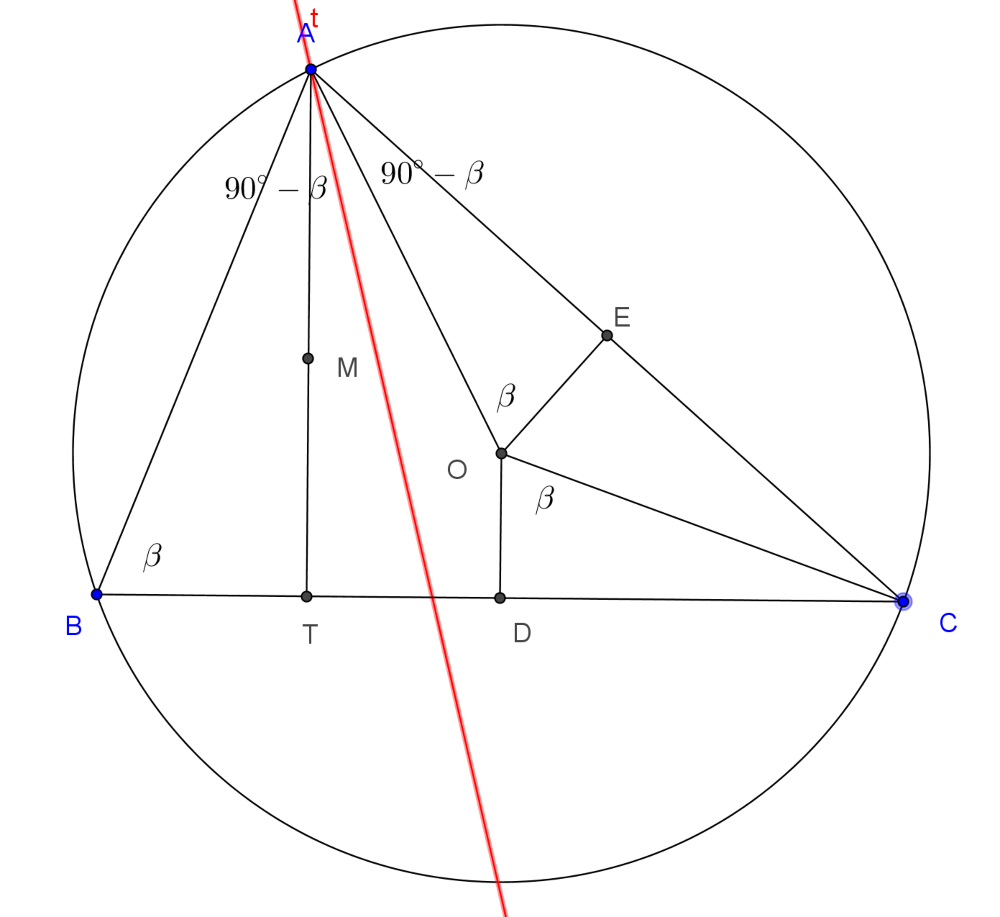
A $\displaystyle BTA$ derékszögű háromszögben $\displaystyle ABT\sphericalangle=\beta$, így a másik hegyesszöge $\displaystyle BAT\sphericalangle=BAM\sphericalangle=90^\circ-\beta$. A háromszög körülírt körét tekintve az $\displaystyle AOC$ középponti szög kétszerese a $\displaystyle B$-nél fekvő kerületi szögnek. Ezt a szöget az $\displaystyle OE$ szakasz felezi, tehát $\displaystyle AOE\sphericalangle=\beta$. Az $\displaystyle AOE$ derékszögű háromszögben ennek megfelelően $\displaystyle OAE\sphericalangle=90^\circ-\beta$. Ezzel beláttuk, hogy a belső szögfelező felezi az $\displaystyle MAO$ szöget is, $\displaystyle MAI\sphericalangle=IAO\sphericalangle=|\frac{\alpha}{2}-90^\circ+\beta|$.

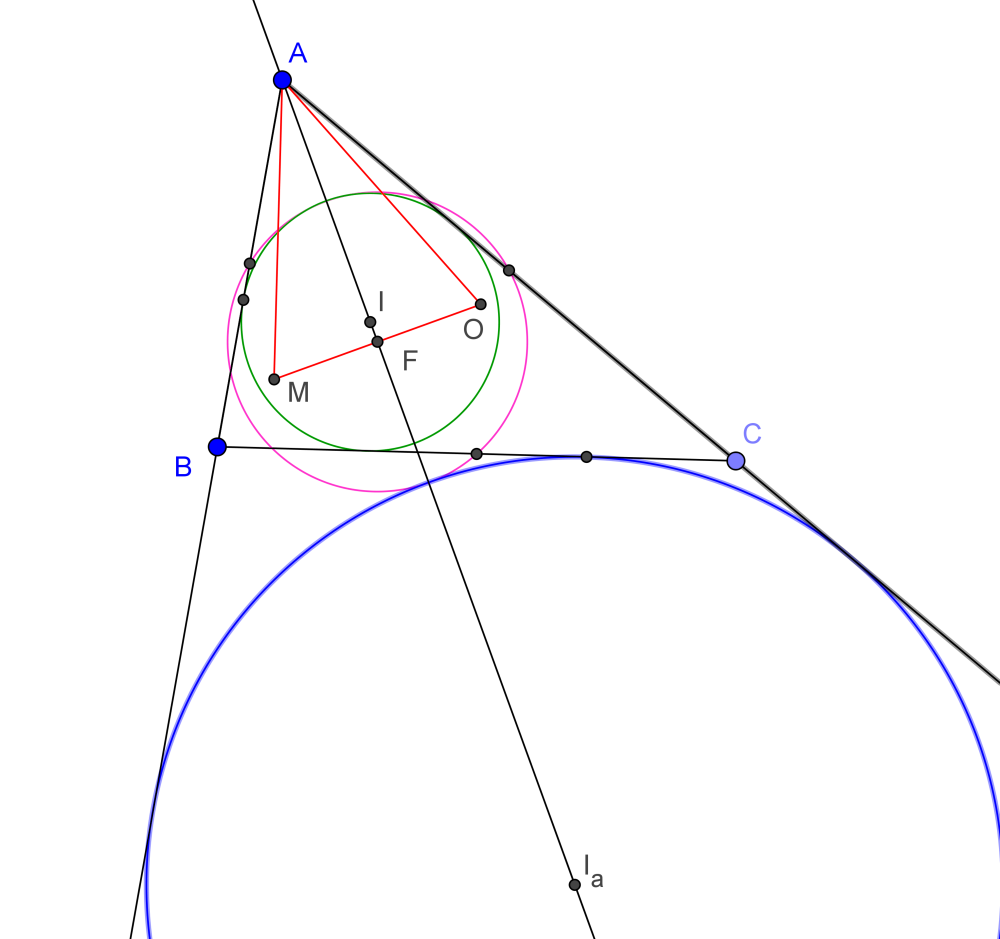
A továbbiakban tekintsük az $\displaystyle I, F$ és $\displaystyle I_a$ pontokat. Ezek általában egy háromszöget határoznak meg. A 4. pontban említett érintések alapján tudjuk, hogy $\displaystyle IF=\frac R2 - r$, továbbá $\displaystyle FI_a=\frac R2 +r_a$. Most a feltételek szerint:

$\displaystyle IF+FI_a=\frac R2-r+\frac R2+r_a=R-r+r_a=II_a.$

Azt kaptuk, hogy a háromszög elfajuló, az $\displaystyle F$ pont az $\displaystyle II_a$ szakaszon helyezkedik el. Ez viszont éppen az $\displaystyle A$-hoz tartozó belső szögfelező.

A Feurbach-kör középpontja ezek szerint rajta van a belső szögfelezőn, amely – ahogy korábban megmutattuk – felezi az $\displaystyle MAO$ szöget. Lévén az $\displaystyle F$ pont az $\displaystyle OM$ szakasz felezőpontja ebből következik, hogy az $\displaystyle MAO$ háromszög egyenlő szárú, $\displaystyle AM=R$.

Végül a 3. számú állítást felhasználva:

$\displaystyle AM=2R\cos\alpha=R, ~~\text{azaz}~~ \cos\alpha=\frac 12, \quad \alpha=60^\circ.$

Statisztika:

39 dolgozat érkezett.
6 pontot kapott:	Ali Richárd, Aravin Peter, Bencze Mátyás, Bodor Ádám, Bui Thuy-Trang Nikolett, Diaconescu Tashi, Gyenes Károly, Hodossy Réka, Holló Martin, Horvath Benedek, Kerekes András, Kovács Benedek Noel, Kővágó Edit Gréta, Li Mingdao, Minh Hoang Tran, Molnár Lili, Pázmándi József Áron, Pletikoszity Martin, Prohászka Bulcsú, Puppi Barna, Sajter Klaus, Sárdinecz Dóra, Sha Jingyuan, Szabó 721 Sámuel, Varga 511 Vivien, Veres Dorottya, Vigh 279 Zalán, Virág Lénárd Dániel, Virág Tóbiás, Vödrös Dániel László, Wágner Márton, Zhai Yu Fan.
3 pontot kapott:	1 versenyző.
1 pontot kapott:	3 versenyző.
0 pontot kapott:	1 versenyző.

A KöMaL 2024. novemberi matematika feladatai