A B. 5424. feladat (2024. december)

B. 5424. Tetszőleges pozitív egész \(\displaystyle n\) esetén \(\displaystyle K_n\)-nel jelöljük azt az alakzatot, amelyet úgy kapunk, hogy egy \(\displaystyle (2n)\times(2n)\) méretű ,,sakktábla'' mind a négy sarkából kivágunk egy-egy \(\displaystyle (n-1)\times(n-1)\) nagyságú négyzetet, az ábráknak megfelelően.

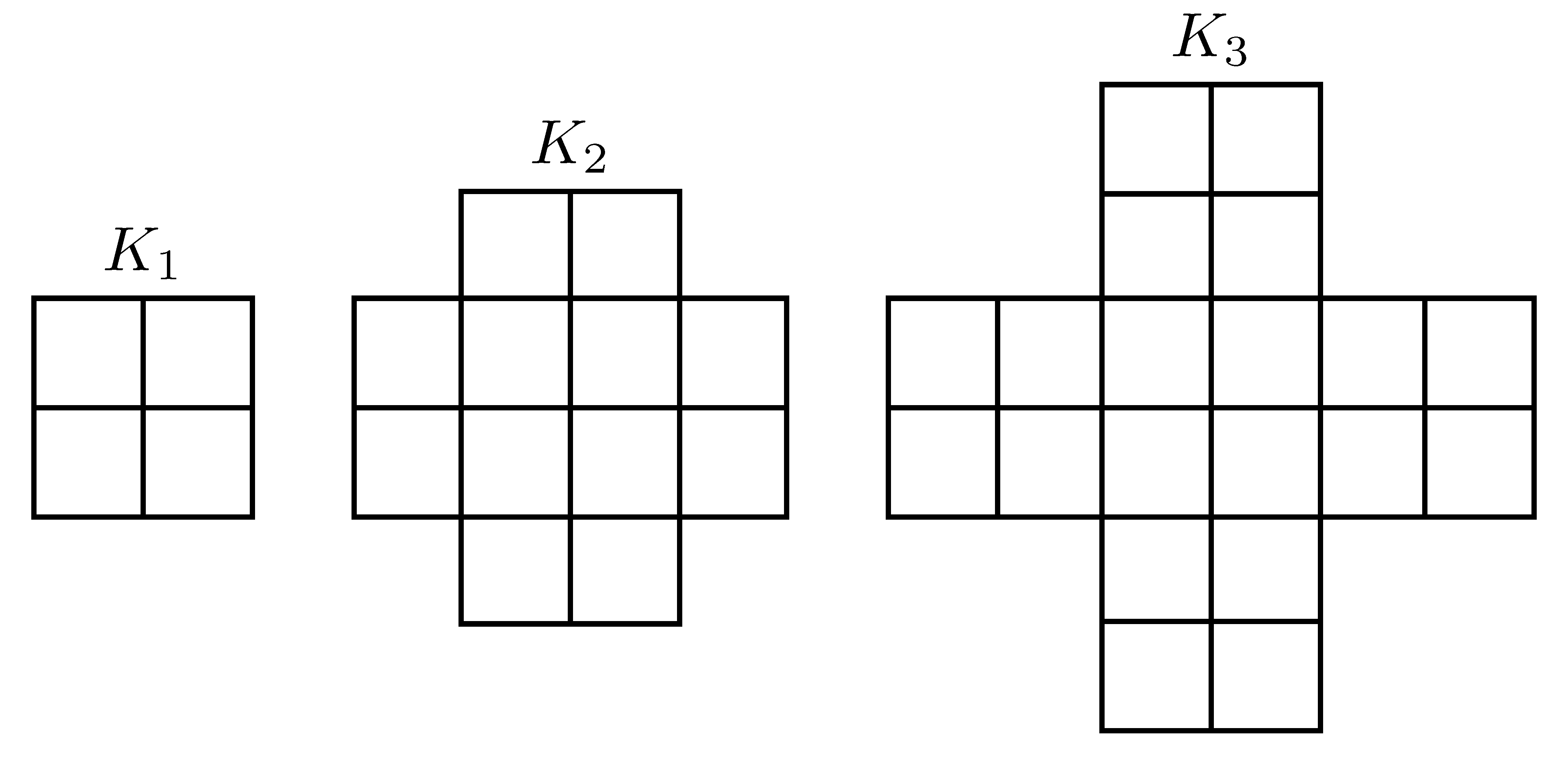
Jelöljük \(\displaystyle a_n\)-nel azt, ahányféleképpen lefedhető \(\displaystyle K_n\) hézag- és átfedésmentesen \(\displaystyle ({2\times 1})\)-es dominókkal. (Például \(\displaystyle a_1=2\), illetve \(\displaystyle a_2=8\).) Igazoljuk, hogy \(\displaystyle 2a_n\) minden \(\displaystyle n\)-re négyzetszám.

Javasolta: Sztranyák Attila (Budapest)

(4 pont)

A beküldési határidő 2025. január 10-én LEJÁRT.

Megoldás. \(\displaystyle K_1\) lefedéseinek a száma 2 (ennek duplája valóban négyzetszám); a továbbiakban foglalkozzunk az ettől ,,nagyobb'' \(\displaystyle K_n\)-ekkel. A könnyebb leírás érdekében tájoljuk az alakzatunkat az égtájok szerint, majd vizsgáljuk a tábla középső \(\displaystyle 2 \times 2\)-es négyzetét. Ennek (az alábbi ábrán ,,sraffozottan'' megjelölt) jobb felső mezőjét nyilván le kell fedni valahogyan, vagy egy függőleges, vagy egy vízszintes dominóval. Tegyük fel, hogy (mint az ábrán) egy függőleges dominóval fedjük le.

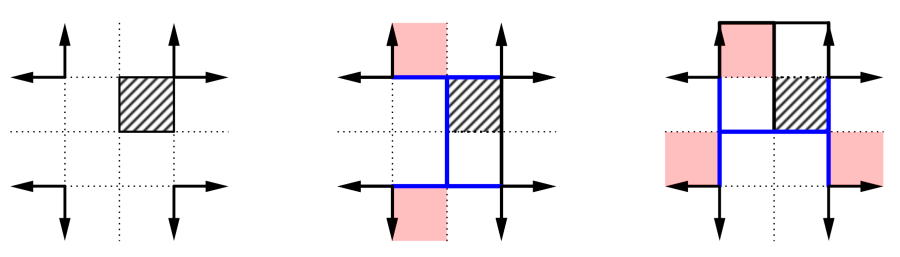
Ekkor két lehetőség van;

– Ha a lefedő dominó a jelölt mezőt és a tőle délre lévő mezőt fedi le (középső ábra), akkor a jelölt mezőtől észak-nyugatra lévő, pirossal jelölt mező nem fedhető le olyan függőleges dominóval, aminek a piros mező az északi mezeje, mert ekkor az alakzat ,,északi'' ágában lévő lefedetlen maradéka páratlan mezőt tartalmazna. Hasonló okokból a középső ábra másik pirossal jelölt mezője sem fedhető le olyan függőleges dominóval, aminek a piros mező a déli mezeje. Ekkor (középső) ábránkon dominószélekből kialakul az ábrán kékkel megrajzolt (elforgatott) H betű.

– Ha pedig a lefedő dominó a jelölt mezőt és a tőle északra lévő mezőt fedi le (jobb oldali ábra), akkor a jelölt mezőtől észak-nyugatra lévő, pirossal jelölt mező csak olyan függőleges dominóval fedhető le, amelynek ez a piros mező az északi mezeje (különben az ,,északi ág maradéka'' megint csak páratlan mezőt tartalmazna); továbbá az előzőekhez hasonlóan az ábrán lévő két további piros mező sem fedhető le olyan dominókkal, aminek a másik mezeje a tábla középső \(\displaystyle 2\times 2\)-es négyzetének valamelyik mezeje. Így ebben az esetben (jobb oldali ábra) is kialakul az iménti, kékkel megrajzolt H betű (csak ,,állva'').

Nyilván ha a jelölt mezőt lefedő dominó vízszintes, akkor is ugyanez a helyzet; azaz az alakzatunk középpontja egyúttal középpontja egy dominószélekből álló \(\displaystyle 2 \times 2\)-es méretű H betűnek is, továbbá a H betű kétféleképpen állhat (,,állva'', vagy ,,elforgatva'').

Ez a H betű kettévágja az alakzatunkat 2 darab \(\displaystyle 2 \times (n-1)\)-es és 2 darab \(\displaystyle 2 \times n\)-es részre, amelyek egymástól függetlenül parkettázhatók. Jelöljük \(\displaystyle g_n\)-nel egy \(\displaystyle 2 \times n\)-es téglalap dominólefedéseinek a számát. Ekkor a fentiek szerint az alakzatunk lefedéseinek a száma \(\displaystyle a_n = 2 \cdot g^2_n \cdot g^2_{n-1} = 2 \left( g_n \cdot g_{n-1} \right)^2\), aminek kétszerese valóban egy négyzetszám.

Megjegyzés: Viszonylag ismert, hogy a \(\displaystyle 2 \times n\)-es téglalap dominólefedéseinek a száma \(\displaystyle g_n=f_{n+1}\) (az \(\displaystyle (n+1)\)-dik Fibonacci szám). Ebből \(\displaystyle K_n\) alakzat lefedéseinek a száma \(\displaystyle a_n= 2 \cdot f^2_{n+1} \cdot f^2_{n}\).

Statisztika:

A B. 5424. feladat értékelése még nem fejeződött be.

A KöMaL 2024. decemberi matematika feladatai