A B. 5425. feladat (2024. december)

B. 5425. Legyen \(\displaystyle ABCD\) húrnégyszög köré írt körének középpontja \(\displaystyle O\), az \(\displaystyle AC\) átlójának felezőpontja pedig \(\displaystyle E\). Tegyük fel továbbá, hogy \(\displaystyle O\) és \(\displaystyle E\) különbözőek. Mutassuk meg, hogy ha \(\displaystyle OEBD\) is húrnégyszög, akkor \(\displaystyle EC\) felezi a \(\displaystyle DEB\) szöget.

Javasolta: Somogyi Ákos (London)

(4 pont)

A beküldési határidő 2025. január 10-én LEJÁRT.

Megoldás. Az \(\displaystyle ABCD\) körben \(\displaystyle OA=OB=OC=OD\) a kör sugarai.

Az \(\displaystyle OAC\) háromszög egyenlő szárú, ezért az \(\displaystyle OE\) egyenes a háromszög magassága: \(\displaystyle AC\perp OE\).

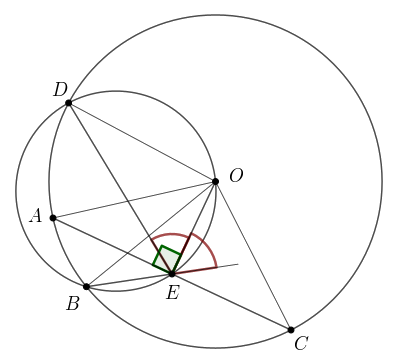
Az \(\displaystyle BEOD\) körben \(\displaystyle BO=DO\) miatt a \(\displaystyle BO\) és \(\displaystyle OD\) ívek egyenlők, ezért \(\displaystyle OE\) a \(\displaystyle BED\) szög külső szögfelezője. A külső szögfelezőre merőleges, a szög csúcsán átmenő \(\displaystyle AEC\) egyenes tehát a \(\displaystyle BED\) szög belső szögfelezője.

Statisztika:

72 dolgozat érkezett.
4 pontot kapott:	66 versenyző.
3 pontot kapott:	4 versenyző.
2 pontot kapott:	1 versenyző.

A KöMaL 2024. decemberi matematika feladatai