A B. 5429. feladat (2024. december)

B. 5429. Tetszőleges $\displaystyle X$, $\displaystyle Y$, $\displaystyle Z$ pontokra jelölje $\displaystyle [XYZ]$ az $\displaystyle XYZ$ háromszög területét. Mutassuk meg, hogy ha az $\displaystyle A$, $\displaystyle B$, $\displaystyle C$, $\displaystyle D$, $\displaystyle E$, $\displaystyle F$ pontok egy nem elfajuló kúpszeletre esnek, akkor

$\displaystyle [ABC]\cdot[CDE]\cdot[EFA]\cdot[BDF]=[BCD]\cdot[DEF]\cdot[FAB]\cdot[ACE]. $

Javasolta: Kós Géza (Budapest)

(6 pont)

A beküldési határidő 2025. január 10-én LEJÁRT.

1. megoldás. Először vizsgáljuk meg, mi történik, ha $\displaystyle A,B,C,D,E,F$ közül valamelyik kettő egybeesik. A pontok szerepe ciklikusan szimmetrikus, ezért elég azt az esetet néznünk, ha $\displaystyle A$ egybeesik egy másik ponttal. Az $\displaystyle AB$, $\displaystyle AC$, $\displaystyle AE$, $\displaystyle AF$ szakaszok az állítás mindkét oldalán szerepelnek valamelyik háromszög oldalaként, ezért ha $\displaystyle A=B$, $\displaystyle A=C$, $\displaystyle A=E$ vagy $\displaystyle A=F$, akkor mindkét szorzat nulla. Ha pedig $\displaystyle A=D$, akkor $\displaystyle [ABC]=[BCD]$ (a két háromszög körüljárása azonos), $\displaystyle [CDE]=[ACE]$ (a két háromszög körüljárása ellentétes), $\displaystyle [EFA]=[DEF]$ (azonos körüjárás) és $\displaystyle [BDF]=[FAB]$ (ellentétes körüljárás), így a két szorzat tényezői ugyanazok, csak a sorrendjükben különböznek. Az állítás tehát mindig teljesül, ha valamelyik két pont egybeesik.

A továbbiakban feltételezzük, hogy $\displaystyle A,B,C,D,E,F$ páronként különböző, így az általuk meghatározott háromszögek nem fajulhatnak el, az állításban szereplő területek egyike sem $\displaystyle 0$.

Jelöljük a kúpszeletet $\displaystyle \Omega$-val. Abban a speciális esetben, ha $\displaystyle \Omega$ egy $\displaystyle r$ sugarú kör, akkor a bizonyítandó állítás két oldalán mindenhol alkalmazzuk a jól ismert $\displaystyle t=\dfrac{abc}{4r}$ területképletet:

$$\begin{gather*} [ABC]\cdot[CDE]\cdot[EFA]\cdot[BDF] =\\ = \dfrac{AB\cdot BC\cdot AC}{4r} \cdot \dfrac{CD\cdot DE\cdot CE}{4r} \cdot \dfrac{EF\cdot FA\cdot EA}{4r} \cdot \dfrac{BD\cdot DF\cdot FB}{4r}, \\ [BCD]\cdot[DEF]\cdot[FAB]\cdot[ACE] =\\ = \dfrac{BC\cdot CD\cdot BD}{4r} \cdot \dfrac{DE\cdot EF\cdot DF}{4r} \cdot \dfrac{FA\cdot AB\cdot FB}{4r} \cdot \dfrac{AC\cdot CE\cdot EA}{4r}. \end{gather*}$$

A jobboldalakon ugyanazoknak a szakaszoknak a szorzata szerepel, tehát ezek egyenlők, ami bizonyítja az állítást.

Az általános esetet úgy bizonyítjuk, hogy a kúpszeletet egy körre vetítjük. Jól ismert, hogy bármely nemelfajuló kúpszelet előáll, egy – mindkét irányban végtelen – kúppalást és egy, a kúp csúcsára nem illeszkedő sík metszeteként. Vegyünk tehát fel egy $\displaystyle O$ csúcsú kúppalástot, amelyre $\displaystyle \Omega$ illeszkedik, és vegyünk fel egy $\displaystyle \Omega'$ kört ugyanezen a kúpon. Ekkor az $\displaystyle O$ pontból az $\displaystyle \Omega$-t az $\displaystyle \Omega'$ körre vetíthetjük.

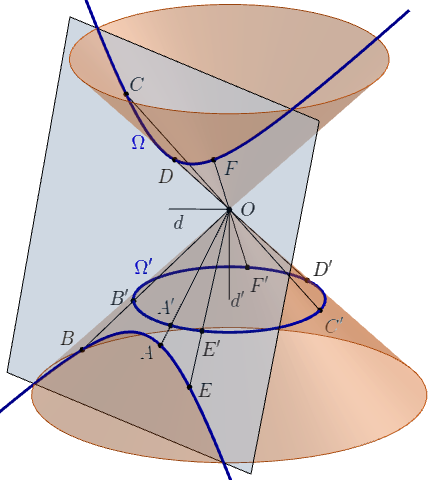
Jelölje az $\displaystyle A,B,C,D,E,F$ pontok képét rendre $\displaystyle A',B',C',D',E',F'$. Legyen továbbá az $\displaystyle O$ pont távolsága $\displaystyle \Omega$ és $\displaystyle \Omega'$ síkjától $\displaystyle d$, illetve $\displaystyle d'$.

A B.5101. feladathoz hasonlóan, bármely $\displaystyle X,Y,Z\in\Omega$ pontokra és ezek $\displaystyle X',Y',Z'\in\Omega'$ képeire tekintsük az $\displaystyle OXYZ$ és az $\displaystyle OX'Y'Z'$ tetraéder térfogatát. A tetraéderek térfogatait $\displaystyle v(...)$-vel jelölve,

$\displaystyle \dfrac{[XYZ]}{[X'Y'Z']} = \dfrac{\dfrac3{d}v(OXYZ)}{\dfrac3{d'}v(OX'Y'Z')} = \dfrac{d'}{d}\cdot\dfrac{v(OXYZ)}{v(OX'Y'Z')} = \dfrac{d'}{d} \cdot\dfrac{OX}{OX'} \cdot\dfrac{OY}{OY'} \cdot\dfrac{OZ}{OZ'}. $

Ha ezt behelyettesítjük a bizonyítandó állítás két oldalán szereplő háromszögek területeibe,

$$\begin{gather*} \dfrac{[ABC]}{[A'B'C']} \cdot\dfrac{[CDE]}{[C'D'E']} \cdot\dfrac{[EFA]}{[E'F'A']} \cdot\dfrac{[BDF]}{[B'D'F']} =\\ =\bigg(\dfrac{d'}{d} \cdot\dfrac{OA}{OA'} \cdot\dfrac{OB}{OB'} \cdot\dfrac{OC}{OC'}\bigg)\cdot \bigg(\dfrac{d'}{d} \cdot\dfrac{OC}{OC'} \cdot\dfrac{OD}{OD'} \cdot\dfrac{OE}{OE'}\bigg) \cdot\\ \cdot \bigg(\dfrac{d'}{d} \cdot\dfrac{OE}{OE'} \cdot\dfrac{OF}{OF'} \cdot\dfrac{OA}{OA'}\bigg) \cdot \bigg(\dfrac{d'}{d} \cdot\dfrac{OB}{OB'} \cdot\dfrac{OD}{OD'} \cdot\dfrac{OF}{OF'}\bigg) =\\ \bigg(\dfrac{d'}{d}\bigg)^4\cdot \bigg(\dfrac{OA}{OA'} \cdot\dfrac{OB}{OB'} \cdot\dfrac{OC}{OC'} \cdot\dfrac{OD}{OD'} \cdot\dfrac{OE}{OE'} \cdot\dfrac{OF}{OF'} \bigg)^2, \end{gather*}$$

és ugyanígy

$\displaystyle \dfrac{[BCD]}{[B'C'D']} \cdot\dfrac{[DEF]}{[D'E'F']} \cdot\dfrac{[FAB]}{[F'A'B']} \cdot\dfrac{[ACE]}{[A'C'E']} = \bigg(\dfrac{d'}{d}\bigg)^4\cdot \bigg(\dfrac{OA}{OA'} \cdot\dfrac{OB}{OB'} \cdot\dfrac{OC}{OC'} \cdot\dfrac{OD}{OD'} \cdot\dfrac{OE}{OE'} \cdot\dfrac{OF}{OF'} \bigg)^2, $

tehát

$\displaystyle \dfrac{[ABC]}{[A'B'C']} \cdot\dfrac{[CDE]}{[C'D'E']} \cdot\dfrac{[EFA]}{[E'F'A']} \cdot\dfrac{[BDF]}{[B'D'F']} = \dfrac{[BCD]}{[B'C'D']} \cdot\dfrac{[DEF]}{[D'E'F']} \cdot\dfrac{[FAB]}{[F'A'B']} \cdot\dfrac{[ACE]}{[A'C'E']}. $

$\displaystyle (1) $

Végül, mivel $\displaystyle A',B',C',D',E',F'$ egy körön vannak, ezekre már igazoltuk, hogy

$\displaystyle [A'B'C']\cdot[C'D'E']\cdot[E'F'A']\cdot[B'D'F']= [B'C'D']\cdot[D'E'F']\cdot[F'A'B']\cdot[A'C'E']. $

$\displaystyle (2) $

Az (1) és (2) szorzata éppen kiadja a bizonyítandó állítást.

Megjegyzések. 1. A megoldás előjeles szakaszokkal, területekkel és térfogatokkal is elmondható, így a feladat állítása előjeles területekkel is igaz.

2. Tetszőleges $\displaystyle A,B,C,D,E,F$ pontok esetén, amelyek közül semelyik három nem esik egy egyenesre, vizsgálhatjuk az

$\displaystyle f(A,B,C,D,E,F) = \frac{[ABC]\cdot[CDE]\cdot[EFA]\cdot[BDF]}{[BCD]\cdot[DEF]\cdot[FAB]\cdot[ACE]} $

kifejezést, ahol most előjeles területeket használunk. A fenti megoldás mutatja, hogy az $\displaystyle f$ függvény – a kettősviszonyhoz hasonlóan – vetítésinvariáns: ha a pontokat középpontosan vetítjük egy másik síkra, akkor az $\displaystyle f$ értéke nem változik, és $\displaystyle f(A,B,C,D,E,F)$ értéke akkor és csak akkor $\displaystyle 1$, ha $\displaystyle A,B,C,D,E,F$ egy kúpszeletre esik.

2. megoldás. Az első megoldáshoz hasonlóan feltehetjük, hogy $\displaystyle A,B,C,D,E,F$ páronként különböző.

Rögzítsük a $\displaystyle B,C,D,E,F$ pontokat, és a sík tetszőleges $\displaystyle X=(x,y)$ pontjára legyen

$\displaystyle f(X) = [XBC]\cdot[CDE]\cdot[EFX]\cdot[BDF]- [BCD]\cdot[DEF]\cdot[FXB]\cdot[XCE], $

ahol most is előjeles területeket használunk. Azt már tudjuk, hogy $\displaystyle f(B)=f(C)=f(D)=f(E)=f(F)=0$; azt kell igazolnunk, hogy $\displaystyle f(A)=0$.

Az $\displaystyle X\mapsto[XBC]$, $\displaystyle X\mapsto[EFX]$, $\displaystyle X\mapsto[FXB]$, $\displaystyle X\mapsto[XCE]$ függvények lineárisak, így $\displaystyle f$ egy kétváltozós, legfeljebb másodfokú polinom. Az $\displaystyle f(X)=0$ ezért vagy egy kúpszelet, vagy egy egyenes egyenlete, vagy pedig azonosság.

Egy kúpszeletet egyértelműen meghatároz 5 különböző pontja, tehát ha $\displaystyle f(X)=0$ egy kúpszelet egyenlete, akkor ez csak az $\displaystyle B,C,D,E,F$ pontokra illeszkedő kúpszelet lehet, amelyre $\displaystyle A$ is illeszkedik, tehát $\displaystyle f(A)=0$.

Mivel a $\displaystyle B,C,D,E,F$ pontok nem esnek egy egyenesre, az $\displaystyle f(X)=0$ nem lehet egyenes egyenlete.

Végül, ha $\displaystyle f(X)=0$ azonosság, akkor az $\displaystyle A$ pontra is automatikusan teljesül.

Statisztika:

A B. 5429. feladat értékelése még nem fejeződött be.

A KöMaL 2024. decemberi matematika feladatai

Már regisztráltál?
Új vendég vagy?