A B. 5439. feladat (2025. február)

B. 5439. Az $\displaystyle ABCD$ téglalapra teljesül, hogy $\displaystyle AD<AB<2AD$. Legyen $\displaystyle O$ az $\displaystyle AB$ oldal azon pontja, amelyre $\displaystyle OB=AD$. Az $\displaystyle O$ középpontú $\displaystyle OB$ sugarú kör az $\displaystyle AD$ oldalt $\displaystyle E$ pontban metszi. Mutassuk meg, hogy $\displaystyle ABCD$ területe $\displaystyle BE^2/2$.

Javasolta: Vígh Viktor (Sándorfalva)

(3 pont)

A beküldési határidő 2025. március 10-én LEJÁRT.

Megoldás. Jelölje a téglalap oldalhosszúságait $\displaystyle AB = CD = a$ és $\displaystyle BC = DA = b$. Ekkor a feltételek szerint $\displaystyle OB = OE = b$ és $\displaystyle AO = a-b$.

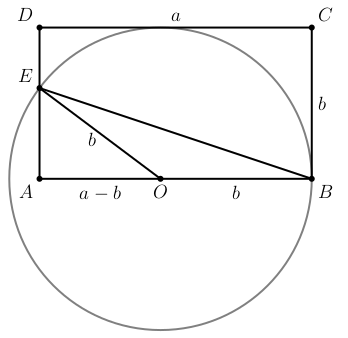
A Pitagorasz-tétel szerint az $\displaystyle AOE$ derékszögű háromszögben:

$\displaystyle AE^2 = OE^2 - AO^2 = b^2 - (a-b)^2 = 2ab - a^2;$

míg az $\displaystyle ABE$ derékszögű háromszögben:

$\displaystyle BE^2 = AB^2 + AE^2 = a^2 + (2ab - a^2) = 2ab,$

azaz valóban az $\displaystyle ABCD$ téglalap területének kétszerese.

Statisztika:

111 dolgozat érkezett.
3 pontot kapott:	98 versenyző.
2 pontot kapott:	7 versenyző.
1 pontot kapott:	3 versenyző.
Nem számítjuk a versenybe a születési dátum vagy a szülői nyilatkozat hiánya miatt:	1 dolgozat.

A KöMaL 2025. februári matematika feladatai