A B. 5440. feladat (2025. február)

B. 5440. Egy háromszög oldalait az oldalegyenesek mentén mindkét irányban meghosszabbítottuk, és mindegyik csúcs után felmértük még a csúccsal szemközti oldal hosszát. Mutassuk meg, hogy az így kapott hat pont egy körre illeszkedik.

Javasolta: Róka Sándor (Nyíregyháza)

(4 pont)

A beküldési határidő 2025. március 10-én LEJÁRT.

1. megoldás. Legyenek a háromszög csúcsai $\displaystyle A$, $\displaystyle B$, $\displaystyle C$; az oldalak hosszúságai a szokásos jelölések szerint $\displaystyle a$, $\displaystyle b$ és $\displaystyle c$. Az $\displaystyle AB$, illetve $\displaystyle AC$ szakaszokra az $\displaystyle A$-n túl felmért $\displaystyle a$ hosszúságú szakaszok másik végpontjai legyenek $\displaystyle M$, illetve $\displaystyle N$. Ugyanezen módon a $\displaystyle B$-n túli meghosszabbítások végpontjai $\displaystyle P$ és $\displaystyle Q$, végül a $\displaystyle C$-n túli meghosszabbítások végpontjai $\displaystyle R$ és $\displaystyle S$ pontok az ábra szerint.

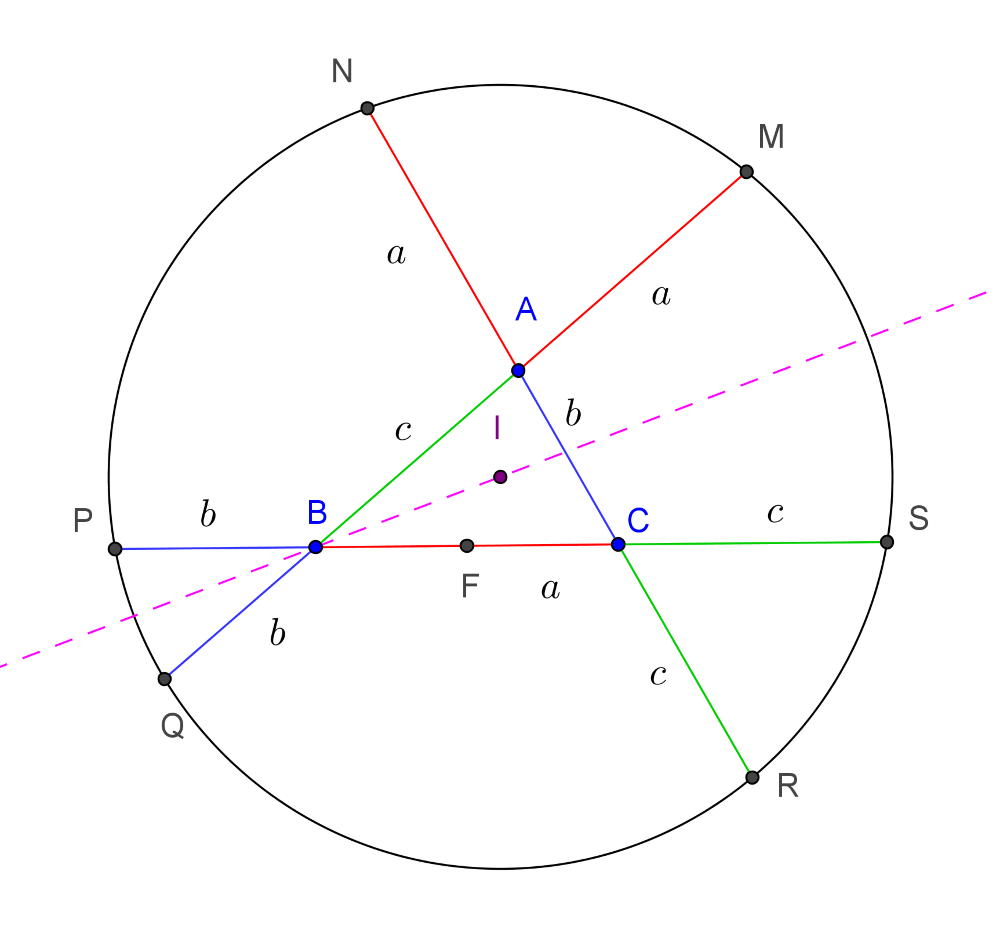
A $\displaystyle BMS$ és $\displaystyle BPQ$ háromszögek egyenlő szárú háromszögek. A $\displaystyle B$ csúcshoz tartozó szögfelezőjük egybeesik. Ennek bármelyik $\displaystyle X$ pontjára $\displaystyle MX=SX$ és $\displaystyle PX=QX$. Ugyanez elmnodható, ha a $\displaystyle B$ csúcs helyett az $\displaystyle A$, illetve a $\displaystyle C$ csúcson átmenő szögfelezőegyenest nézzük. A szögfelezőegyenesek $\displaystyle I$ metszéspontjára – az $\displaystyle ABC$ háromszög beírt körének középpontjára – teljesül, hogy $\displaystyle IM=IS$ és $\displaystyle IP=IQ$; $\displaystyle IM=IN$ és $\displaystyle I=IR$; $\displaystyle IR=IS$ és $\displaystyle IP=IN$. Az $\displaystyle I$ pont egyenlő távolságra van mind a hat ponttól, a hat pont az $\displaystyle I$ körüli körön helyezkedik el.

2. megoldás. Legyen az $\displaystyle ABC$ háromszög félkerülete $\displaystyle s$. Az első megoldás jelöléseit megtartva látjuk, hogy az $\displaystyle MQ$, $\displaystyle NR$ és $\displaystyle PS$ szakaszok hossza megegyezik az $\displaystyle ABC$ háromszög kerületével. Három egyforma hosszúságú szakasz csak úgy lehet egy kör három húrja, ha felezőmerőlegeseik átmennek egy közös ponton, és ettől a ponttól mind egyforma távolságra vannak. Legyen $\displaystyle PS$ felezőpontja $\displaystyle F$. Az $\displaystyle FP$ távolság $\displaystyle s$, ennek megfelelően $\displaystyle FB=s-b$, azaz az $\displaystyle F$ pont az $\displaystyle ABC$ háromszög beírt körének érintési pontja a $\displaystyle BC$ oldalon. Az erre állított merőleges éppen a beírt kör sugarára illeszkedik. Igaz ez a másik két oldal esetében is, ezzel beláttuk, hogy a három felezőmerőleges a beírt kör $\displaystyle I$ középpontjában metszi egymást, ami nyilván egyenlő távolságra van mindhárom oldalegyenestől. Ezzel az állítást beláttuk. Azt is látjuk, hogy az $\displaystyle M$, $\displaystyle N$, $\displaystyle P$, $\displaystyle Q$, $\displaystyle R$, $\displaystyle S$ pontok köré írt kör sugara $\displaystyle \sqrt{s^2+r^2}$, ahol $\displaystyle r$ az $\displaystyle ABC$ háromszög beírt körének sugara.

Statisztika:

97 dolgozat érkezett.
4 pontot kapott:	87 versenyző.
3 pontot kapott:	2 versenyző.
2 pontot kapott:	1 versenyző.
1 pontot kapott:	1 versenyző.
0 pontot kapott:	3 versenyző.

A KöMaL 2025. februári matematika feladatai