A B. 5444. feladat (2025. február)

B. 5444. Az $\displaystyle ABCDEF$ húrhatszögben az $\displaystyle AD$ és $\displaystyle CF$ átlók metszéspontja $\displaystyle P$, az $\displaystyle AE$ és a $\displaystyle BF$ metszéspontja pedig $\displaystyle Q$. Mutassuk meg, hogy ha $\displaystyle BC=CP$ és $\displaystyle DP=DE$, akkor $\displaystyle PQ$ felezi a $\displaystyle BQE$ szöget.

Javasolta: Kós Géza (Budapest)

(6 pont)

A beküldési határidő 2025. március 10-én LEJÁRT.

1. megoldás. Legyen $\displaystyle B'$ és $\displaystyle E'$ a másik két pont a körülírt körön, amire $\displaystyle BC=B'C=CP$, illetve $\displaystyle DE=DE'=DP$.

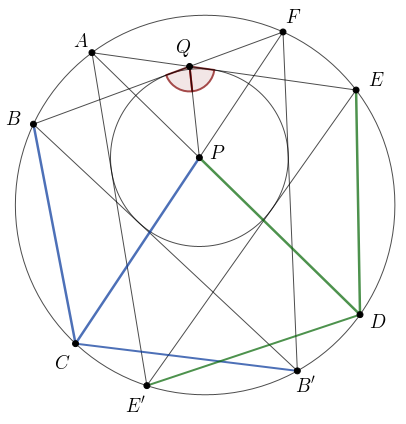
A $\displaystyle BB'F$ háromszögben a $\displaystyle P$ pont az $\displaystyle FC$ szögfelezőnek az a pontja, amelyre $\displaystyle {BC=B'C=CP}$, tehát $\displaystyle P$ a beírt kör középpontja. (Lásd pl. a B. 5291. feladat 1. megoldását.) Ugyanígy, az $\displaystyle AEE'$ háromszögbe írt kör középpontja is $\displaystyle P$.

A $\displaystyle BB'F$ és az $\displaystyle AEE'$ háromszög körülírt köre ugyanaz, és a beírt kör középpontja is. Például az Euler-féle $\displaystyle d^2=r(r-2\varrho)$ képlet miatt a két háromszög beírt köre is ugyanakkora sugarú. Emiatt $\displaystyle QE$ és $\displaystyle QB$ a közös beírt kör két érintője, és $\displaystyle QP$ felezi a $\displaystyle BQE\sphericalangle$-et.

2. megoldás. Legyen a körülírt kör sugara $\displaystyle r$, ekkor az $\displaystyle FBC$ és az $\displaystyle ADE$ háromszögben $\displaystyle \dfrac{BC}{\sin BFC\sphericalangle}=\dfrac{DE}{\sin DAE\sphericalangle}=2r$. Az $\displaystyle APQ$ és a $\displaystyle QPF$ háromszögben a szinusztétel szerint $\displaystyle \dfrac{AP}{\sin AQP\sphericalangle}=\dfrac{PQ}{\sin PAQ\sphericalangle}=\dfrac{PQ}{\sin DAE\sphericalangle}$, illetve $\displaystyle \dfrac{PF}{\sin PQF\sphericalangle}=\dfrac{PQ}{\sin QFP\sphericalangle}=\dfrac{PQ}{\sin BFC\sphericalangle}$. A $\displaystyle P$ pontnak a körülírt körre vonatkozó hatványa $\displaystyle -PA\cdot PD=-PC\cdot PF$. Mindezeket felhasználva

$\displaystyle \sin AQP\sphericalangle =\dfrac{AP\cdot\sin DAE\sphericalangle}{PQ} =\dfrac{AP \cdot DE}{PQ\cdot2r} =\dfrac{AP \cdot PD}{PQ\cdot2r}$

$\displaystyle =\dfrac{PF \cdot PC}{PQ\cdot2r} =\dfrac{PF \cdot BC}{PQ\cdot2r} =\dfrac{PF\cdot\sin BFC\sphericalangle}{PQ} =\sin PQF\sphericalangle.$

Ebből az állítás azonnal következik.

Statisztika:

13 dolgozat érkezett.
6 pontot kapott:	Aravin Peter, Holló Martin, Li Mingdao, Sha Jingyuan, Virág Lénárd Dániel, Virág Tóbiás.
3 pontot kapott:	1 versenyző.
0 pontot kapott:	6 versenyző.

A KöMaL 2025. februári matematika feladatai