A B. 5446. feladat (2025. március)

B. 5446. Mekkora lehet $\displaystyle \ell$, ha egybevágóság erejéig pontosan háromféle háromszög létezik, amelynek egyik oldala egységnyi, egy másik oldala $\displaystyle \ell$ hosszú, és valamelyik szöge 60 fokos?

Javasolta: Hujter Bálint (Budapest)

(3 pont)

A beküldési határidő 2025. április 10-én LEJÁRT.

Megoldás. Három esetet kell vizsgálnunk aszerint, hogy a 60 fokos szög a két adott oldalhoz képest hol helyezkedik el.

1. eset: az egységnyi és az $\displaystyle \ell$ hosszú oldalak $\displaystyle 60^\circ$-t zárnak be. Ezekkel az adatokkal minden $\displaystyle \ell>0$ esetén egybevágóság erejéig pontosan egy háromszög szerkeszthető.

2. eset: a $\displaystyle 60^\circ$ az $\displaystyle \ell$ hosszú oldallal szemben van. Végezzük el a szerkesztést a szokásos módon, lásd ábra. Vegyük fel az $\displaystyle AB$ egységnyi hosszúságú szakaszt, szerkesszünk $\displaystyle A$ pontnál $\displaystyle 60^\circ$-os félegyenest, és ezt messük $\displaystyle B$ körüli $\displaystyle \ell$ sugarú körrel. A félegyenes távolsága $\displaystyle B$ ponttól $\displaystyle \sqrt 3 /2$, ezért nem kapunk megoldást, ha $\displaystyle \ell<\sqrt 3/2$; ha $\displaystyle \ell=\sqrt 3 /2$, akkor pontosan egy megoldás van; ha $\displaystyle \sqrt 3 /2< \ell < 1$, akkor a kör két pontban metszi a félegyenest, ezért két különböző megoldást kapunk. Ha $\displaystyle \ell\ge 1$, akkor az egyik metszéspont megszűnik ($\displaystyle \ell=1$ esetben $\displaystyle A$-val egybeesik, $\displaystyle \ell>1$ esetén kívül esik a félegyenesen), így ismét egy megoldást kapunk.

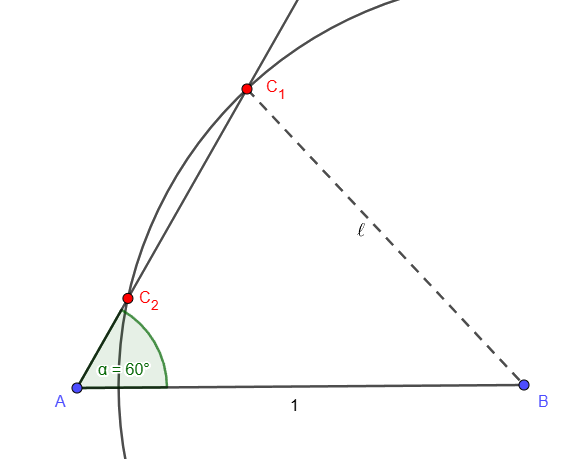
3. eset: a $\displaystyle 60^\circ$ az $\displaystyle 1$ hosszú oldallal szemben van. Ugyanúgy járunk el, mint a 2. esetben. Itt $\displaystyle B$ pont és a félegyenes távolsága $\displaystyle \ell \sqrt 3/2$. Nincs megoldás, ha $\displaystyle 1<\ell \sqrt 3/2$, azaz $\displaystyle \ell> 2/\sqrt 3$. Pontosan egy megoldás van, ha $\displaystyle \ell=2/\sqrt 3$ vagy $\displaystyle \ell\le 1$. Végül két különböző megoldást kapunk, ha $\displaystyle 1<\ell<2/\sqrt 3$.

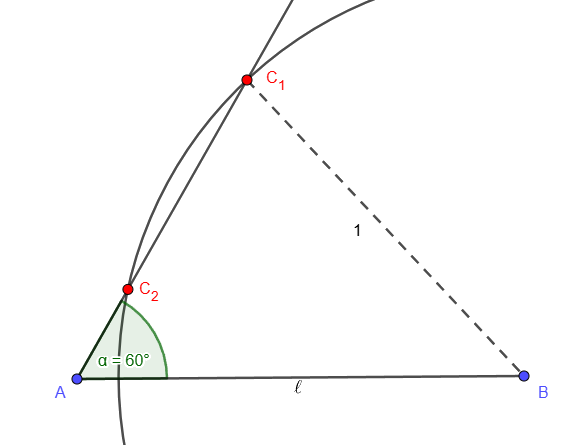
Legalább három különböző háromszöget a fentiek miatt csak akkor kaphatunk, ha $\displaystyle \sqrt 3/2\le \ell \le 2/\sqrt 3.$

Vegyük észre, hogy ha valamely kiszerkesztett háromszög egyenlő szárú, akkor szükségképpen szabályos, és $\displaystyle \ell=1$. Következésképpen ha $\displaystyle \ell \neq 1$, akkor a kiszerkesztett háromszögek egyike sem lehet egyenlő szárú, azaz egyetlen $\displaystyle 60$ fokos szöge van. Ezek szerint, ha $\displaystyle \sqrt 3 /2< \ell < 1$ vagy $\displaystyle 1<\ell<2/\sqrt 3$, akkor mind a négy kapott megoldás páronként nem egybevágó, hiszen vagy a $\displaystyle 60$ fokkal szemközti oldalaik különböznek, vagy a megfelelő esetben tárgyaltak miatt nem egybevágóak.

Világos, hogy $\displaystyle \ell=1$ esetén a szabályos háromszög az egyetlen megoldás. Maradt tehát $\displaystyle \ell =\sqrt 3 /2$ és $\displaystyle \ell = 2/\sqrt 3$, ezekre az előbbi megjegyzés szerint valóban pontosan három különböző megoldás létezik.

Az $\displaystyle \ell$ értéke tehát $\displaystyle \sqrt3 /2$ vagy $\displaystyle 2/\sqrt 3$ lehet.

Statisztika:

78 dolgozat érkezett.
3 pontot kapott:	Ali Richárd, Balaskó Noémi, Balla Ignác , Baran Júlia, Baranyi Ernő, Bencze Mátyás, Blaskovics Ádám, Bodor Ádám, Bogdán Balázs Ákos, Bolla Donát Andor, Bővíz Dániel, Bui Thuy-Trang Nikolett, Csató Hanna Zita , Dancs Bálint, Diaconescu Tashi, Faddi Csongor, Gál Mózes, Hajba Milán, Hajszter Dóra, Hideg János, Hodossy Réka, Holló Martin, Illés Dóra, Járdánházi-Kurutz Vilmos, Jurácsik Marcell, Klement Tamás, Kővágó Edit Gréta, Kriston Regő Márton, Kun Zsófia, Kurucz Lilien Jázmin, Li Mingdao, Mikó Hédi Irma, Miszori Gergő, Molnár Lili, Molnár-Sáska Tamás, Nagypál Katóca, Péter Hanna, Rajtik Sándor Barnabás, Sajter Klaus, Sánta Gergely Péter, Sárdinecz Dóra, Sun Wen Ze, Sütő Áron, Szabó 721 Sámuel, Török Eszter Júlia, Vályi Nagy Ádám András, Varga 511 Vivien, Wágner Márton, Wiener Marcell, Zhai Yu Fan.
2 pontot kapott:	16 versenyző.
1 pontot kapott:	10 versenyző.

A KöMaL 2025. márciusi matematika feladatai