A B. 5451. feladat (2025. március)

B. 5451. Az $\displaystyle ABCD$ konvex négyszögben $\displaystyle BAC\sphericalangle=2 CAD\sphericalangle$, $\displaystyle ADB\sphericalangle=2DBA\sphericalangle$ és $\displaystyle CBD \sphericalangle=30^{\circ}$. Mekkora lehet a $\displaystyle DCA \sphericalangle$?

Kovács Béla (Szatmárnémeti) ötletéből

(5 pont)

A beküldési határidő 2025. április 10-én LEJÁRT.

1. megoldás. Használjuk az ábra jelöléseit, legyen $\displaystyle CAD\sphericalangle=\alpha$ és $\displaystyle DBA\sphericalangle=\beta$. Az $\displaystyle ABD$ háromszögben összeszámolva a szögeket kapjuk, hogy $\displaystyle 3\alpha+3\beta=180^\circ$, azaz $\displaystyle \alpha+\beta= 60^\circ$. Innen az $\displaystyle ABC$ háromszögben

$\displaystyle BCA\sphericalangle=180^\circ-2\alpha-(\beta+30^\circ)=90^\circ -\alpha=30^\circ+\beta,$

azaz az $\displaystyle ABC$ háromszög $\displaystyle BC$ oldalán fekvő szögei egyenlőek, így $\displaystyle AB=AC$, az $\displaystyle A$-ból induló szögfelező pedig magasságvonal is, talppontja legyen $\displaystyle T$. Világos, hogy $\displaystyle CT=BC/2$.

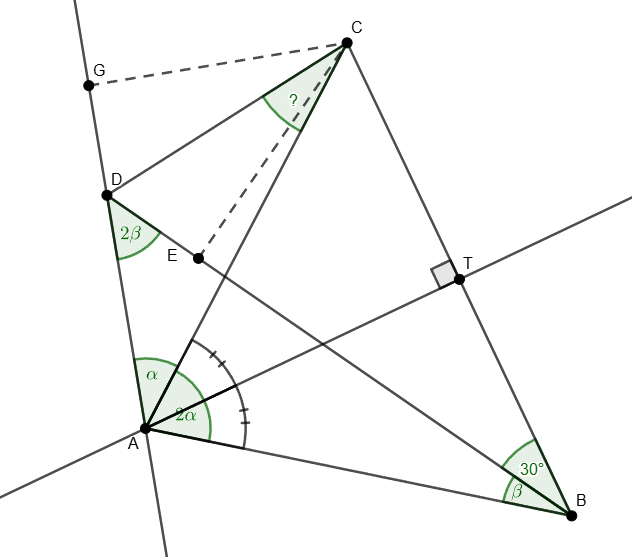
Bocsássunk merőlegest $\displaystyle C$ pontból $\displaystyle BD$ egyenesre, ennek talppontja legyen $\displaystyle E$. A $\displaystyle BCE$ derékszögű háromszögben $\displaystyle B$-nél $\displaystyle 30^\circ$ van, ezért $\displaystyle CE=BC/2=CT$, azaz $\displaystyle C$ pont ugyanolyan távolságra van $\displaystyle AT$ és $\displaystyle BD$ egyenesektől.

Másrészt $\displaystyle TAC\sphericalangle=\alpha=CAD\sphericalangle$, azaz $\displaystyle AC$ szögfelező, így $\displaystyle C$ pont ugyanolyan távolságra $\displaystyle AD$ és $\displaystyle AT$ egyenesektől. Kaptuk tehát, hogy $\displaystyle C$ pont egyenlő távolságra van $\displaystyle BD$ és $\displaystyle AD$ egyenesektől (az ábrán $\displaystyle CE=CG$). Az $\displaystyle ABCD$ négyszög konvexitása miatt $\displaystyle C$ csak $\displaystyle BDG\sphericalangle$ szögfelezőjén lehet.

Innen $\displaystyle BDC\sphericalangle=(180^\circ-ADB\sphericalangle)/2=90^\circ-\beta$, és $\displaystyle ACD$ háromszögben szöget számolva, kihasználva $\displaystyle \alpha+\beta=60^\circ$ összefüggést kapjuk, hogy a keresett szög

$\displaystyle DCA\sphericalangle=180^\circ-\alpha-(2\beta+90^\circ-\beta)=90^\circ-(\alpha+\beta)=30^\circ.$

2. megoldás. Legyen az $\displaystyle ADB\sphericalangle$ felezője és $\displaystyle AC$ metszéspontja $\displaystyle I$, a $\displaystyle BAC\sphericalangle$ felezője és $\displaystyle BC$ metszéspontja $\displaystyle K$.

Ugyanúgy, mint az első megoldásban, $\displaystyle CBA\sphericalangle=ACB\sphericalangle$, $\displaystyle AB=AC$, és ezért $\displaystyle DKA\sphericalangle=60^\circ$, valamint $\displaystyle ACK\sphericalangle=KBA\sphericalangle$.

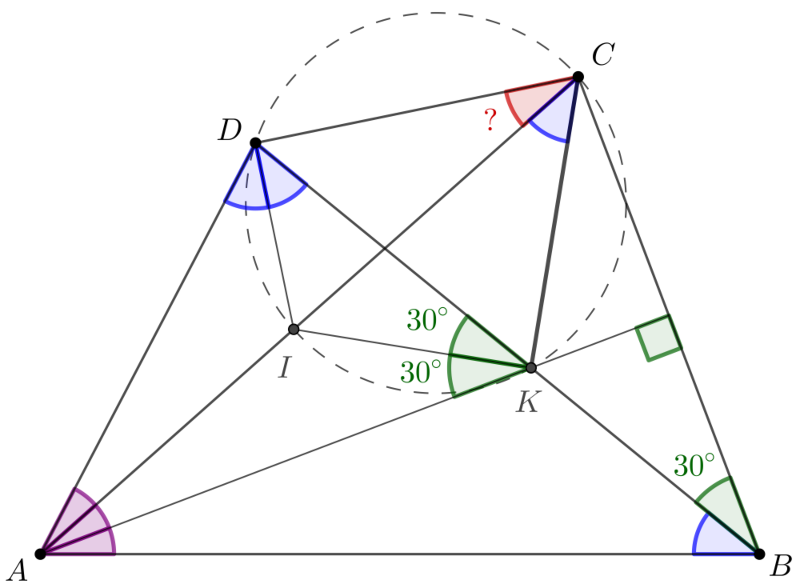
Az $\displaystyle AKD$ háromszögben $\displaystyle I$ az $\displaystyle A$-ból és $\displaystyle D$-ből induló szögfelezők metszéspontja, tehát $\displaystyle I$ a háromszögbe írt kör középpontja, és $\displaystyle KI$ az $\displaystyle I$-ből induló szögfelező: $\displaystyle DKI\sphericalangle =\frac12DKA\sphericalangle =30^\circ$.

Mivel $\displaystyle IDK\sphericalangle=DBA\sphericalangle=ACK\sphericalangle$, így $\displaystyle CDIK$ húrnégyszög, és $\displaystyle DCA\sphericalangle=DKI\sphericalangle=30^\circ$.

Statisztika:

41 dolgozat érkezett.
5 pontot kapott:	Ali Richárd, Aravin Peter, Bui Thuy-Trang Nikolett, Csató Hanna Zita , Diaconescu Tashi, Hajba Milán, Hideg János, Hodossy Réka, Holló Martin, Kerekes András, Pázmándi József Áron, Rajtik Sándor Barnabás, Sajter Klaus, Sárdinecz Dóra, Sha Jingyuan, Sütő Áron, Szabó 721 Sámuel, Török Eszter Júlia, Varga 511 Vivien, Vigh 279 Zalán, Wágner Márton.
4 pontot kapott:	Bencze Mátyás, Bodor Ádám, Kővágó Edit Gréta, Li Mingdao, Sánta Gergely Péter.
3 pontot kapott:	2 versenyző.
2 pontot kapott:	6 versenyző.
1 pontot kapott:	3 versenyző.
0 pontot kapott:	3 versenyző.

A KöMaL 2025. márciusi matematika feladatai