A B. 5452. feladat (2025. március)

B. 5452. Az $\displaystyle F$ fókuszpontú parabolán kijelöltük a $\displaystyle P_1$, $\displaystyle P_2$, $\displaystyle \ldots$, $\displaystyle P_n$ pontokat ($\displaystyle {n\geq 3}$) úgy, hogy

$\displaystyle P_1FP_2\sphericalangle=P_2FP_3\sphericalangle=\ldots=P_nFP_1\sphericalangle=\frac{360^\circ}{n}.$

Bizonyítsuk be, hogy az $\displaystyle FP_1$, $\displaystyle \ldots$, $\displaystyle FP_n$ távolságok harmonikus közepe a parabola paraméterével egyenlő.

Javasolta: Holló Gábor (Budapest)

(6 pont)

A beküldési határidő 2025. április 10-én LEJÁRT.

Megoldás. A megoldás során a szögek értékét radiánban adjuk meg.

Először is bebizonyítjuk az alábbi ismert lemmát:

Tetszőleges $\displaystyle n>1$ egész és valós $\displaystyle \varphi$ esetén $\displaystyle \sin {\varphi }+\sin {\left(\varphi + \frac{2 \pi}{n} \right)}+\sin {\left(\varphi + 2 \cdot \frac{2 \pi}{n} \right)}+\cdots + \sin {\left(\varphi + (n-1) \cdot \frac{2 \pi}{n} \right)}= 0$.

A lemma az alábbi ismert trigonometrikus összegzési képlet egyszerű következménye: tetszőleges $\displaystyle n$ pozitív egész esetén $\displaystyle \sin {\varphi }+\sin {(\varphi +\alpha )}+\sin {(\varphi +2\alpha )}+\cdots +\sin {(\varphi +(n-1)\alpha )}=\frac {{\sin {\left({\frac {n\alpha }{2}}\right)}}\cdot \sin \left(\varphi +{\frac {(n-1)\alpha }{2}} \right)}{ \sin {\frac {\alpha }{2}}}$.

Ha ugyanis ebbe az összegzési képletbe $\displaystyle \alpha = \frac{2 \pi}{n}$-t helyettesítünk éppen a bizonyítandó lemmát kapjuk.

Ettől van elegánsabb bizonyítás is a lemmára, most ezt is megmutatjuk.

A lemma (második) bizonyítása során komplex számokkal dolgozunk. Tekintsük a $\displaystyle z = \cos \varphi + i \sin \varphi$ komplex számot, és ezt szorozzuk meg rendre az $\displaystyle \varepsilon_0=1; \varepsilon_1= \cos \frac{2 \pi}{n} + i \sin \frac{2 \pi}{n}; ... ;\varepsilon_{n-1}= \cos \frac{2 (n-1) \pi}{n} + i \sin \frac{2 (n-1)\pi}{n}$ számokkal, azaz az $\displaystyle n$-dik komplex egységgyökökkel. Jelölje a $\displaystyle z \cdot \varepsilon_k$ szorzatot $\displaystyle z_k$ (így például $\displaystyle z=z_0$), és adjuk össze a $\displaystyle z_0+ z_1+ ... + z_{n-1}$ számokat kétféle módon is.

Először: $\displaystyle z_0+ z_1+ ... + z_{n-1} = z (\varepsilon_0 + \varepsilon_1 + ... + \varepsilon_{n-1}) = 0$, hiszen az $\displaystyle n$-edik egységgyökök összege $\displaystyle n>1$ esetén éppen 0. Mivel az összeg értéke 0, valós és képzetes része is 0.

Másodszor (mivel trigonometrikus alakban megadott komplex számokat szorzunk össze): $\displaystyle z_k=z \cdot \varepsilon_k= \cos {\left(\varphi + \frac{2 k \pi}{n} \right)} + i \cdot \sin {\left(\varphi + \frac{2 k\pi}{n} \right)}$, és így $\displaystyle z_0+ z_1+ ... + z_{n-1}= \cos \varphi + i \cdot \sin \varphi + \cos {\left(\varphi + \frac{2 \pi}{n} \right)} + i \cdot \sin {\left(\varphi + \frac{2 \pi}{n} \right)} + ... + \cos {\left(\varphi + \frac{2 (n-1) \pi}{n} \right)} + i \cdot \sin {\left(\varphi + \frac{2 (n-1)\pi}{n} \right)}$. Ennek az összegnek a képzetes része pedig éppen $\displaystyle \sin {\varphi }+\sin {\left(\varphi + \frac{2 \pi}{n} \right)}+\sin {\left(\varphi + 2 \cdot \frac{2 \pi}{n} \right)}+\cdots + \sin {\left(\varphi + (n-1) \cdot \frac{2 \pi}{n} \right)}$, ami az első összegzés alapján pontosan 0.

Ezzel a lemmát (komplex számok segítségével is) beláttuk. (A bizonyításokból természetesen következik – mivel az összeg valós része is 0 – a lemmához hasonló ,,koszinuszos'' összefüggés is.)

Ezután térjünk rá magára a feladatra; az általánosság megszorítása nélkül feltehetjük, hogy a $\displaystyle p$ paraméterű parabolánk – az alábbi ábrának megfelelően, ahol az $\displaystyle n=5$ esetet ábrázoltuk – fókuszpontja $\displaystyle F(0;\frac{p}{2})$, vezéregyenesének egyenlete $\displaystyle y=-\frac{p}{2}$, továbbá jelölje $\displaystyle FP_1$ félegyenese és az $\displaystyle x$-tengely (pozitív fele) által bezárt szöget $\displaystyle \varphi \neq \frac{\pi}{2}$. (A feladat szövege alapján a többi $\displaystyle P_k$ pont esetén hasonlóan definiálható $\displaystyle \varphi_k = \varphi + (k-1) \cdot \frac{2 \pi}{n}$ szögek is különböznek $\displaystyle \frac{\pi}{2}$-től. )

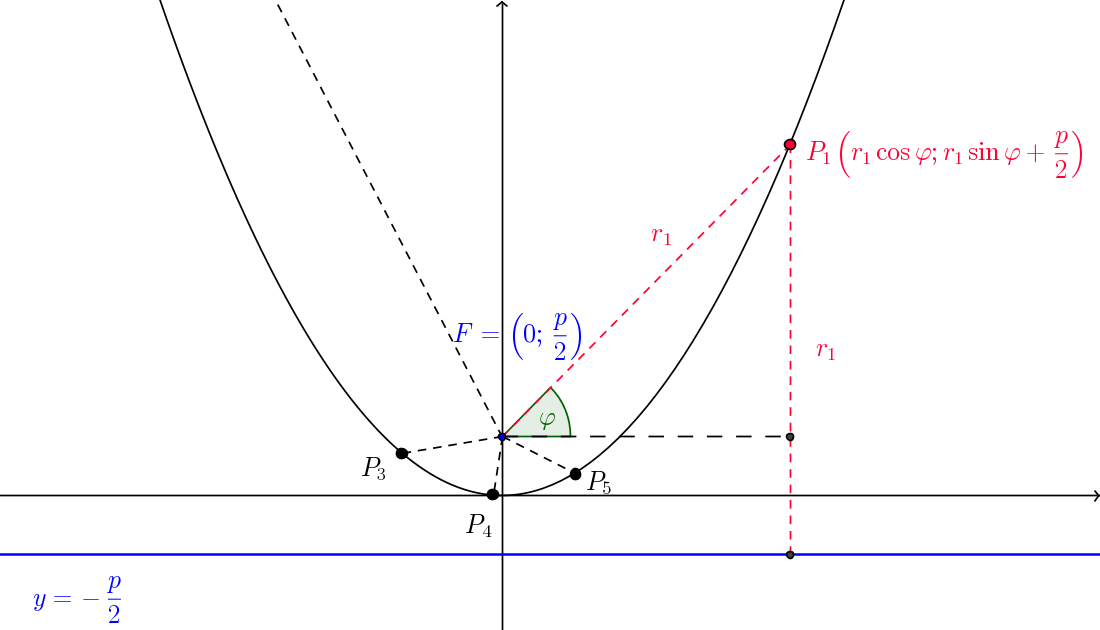
Ha az $\displaystyle FP_1$ távolságot $\displaystyle r_1$-gyel jelöljük, akkor $\displaystyle P_1$ kordinátáira teljesül $\displaystyle P_1\left( r_1 \cos \varphi; r_1 \sin \varphi + \frac{p}{2} \right)$, másfelől a parabola definíciója alapján $\displaystyle r_1$ éppen megegyezik $\displaystyle P_1$-nek a vezéregyenestől vett távolságával, amiből következik, hogy $\displaystyle r_1 = r_1 \sin \varphi + \frac{p}{2} + \frac{p}{2} = r_1 \sin \varphi +p$, innen adódik, hogy $\displaystyle r_1(1 - \sin \varphi) = p$ és végül $\displaystyle \dfrac{1}{r_1} = \dfrac{1 - \sin \varphi}{p}$.

A többi $\displaystyle FP_i=r_i$ távolságra (a feladat feltételei alapján) hasonlóan adódik, hogy $\displaystyle \dfrac{1}{r_i} = \dfrac{1 - \sin \left(\varphi + (i-1)\cdot \frac{2 \pi}{n} \right)}{p}$.

Az eddigiek alapján az $\displaystyle r_i=FP_i$ távolságok harmonikus közepe

$\displaystyle H(r_1;r_2;...;r_n) = \dfrac{n}{\frac{1}{r_1} + \frac{1}{r_2} + ... + \frac{1}{r_n}} = \dfrac{np}{(1 - \sin \varphi) + \left(1 - \sin \left(\varphi + 1 \cdot \frac{2 \pi}{n} \right) \right) + ... + \left(1 - \sin \left(\varphi + (n-1) \cdot \frac{2 \pi}{n} \right) \right)} =$

$\displaystyle =\dfrac{np}{n- \left(\sin \varphi + \sin \left(\varphi + 1 \cdot \frac{2 \pi}{n} \right) + ... + \sin \left(\varphi + (n-1) \cdot \frac{2 \pi}{n} \right) \right)} .$

Az utolsó alak nevezőjében pedig a zárójelben az elsőként igazolt összefüggés alapján éppen $\displaystyle 0$ áll. De akkor $\displaystyle H(r_1;r_2;...;r_n) =\dfrac{np}{n}=p$ adódik, tehát az $\displaystyle FP_1$, $\displaystyle \ldots$, $\displaystyle FP_n$ távolságok harmonikus közepe valóban a parabola paraméterével egyenlő.

Megjegyzés: Ha megengedjük, hogy valamely $\displaystyle i$-re $\displaystyle \varphi_i = \dfrac{\pi}{2}$ és így a hozzá tartozó $\displaystyle P_i$ az ,,ideális'', végtelen távoli pont legyen, akkor az ehhez tartozó $\displaystyle \dfrac{1}{r_i}$-t természetes módon $\displaystyle 0$-nak tekintve továbbra is igaz marad a feladat állítása ezzel a ,,kitejesztett harmonikus középpel''.

Statisztika:

A B. 5452. feladat értékelése még nem fejeződött be.

A KöMaL 2025. márciusi matematika feladatai