A B. 5453. feladat (2025. március)

B. 5453. Egy konvex polidéder lapjai az $\displaystyle ABCD$, $\displaystyle ABFE$, $\displaystyle BCGF$, $\displaystyle CDHG$, $\displaystyle ADHE$ és $\displaystyle EFGH$ négyszögek az ábra szerint. Az $\displaystyle A$, illetve a $\displaystyle G$ csúcsból induló élek páronként merőlegesek egymásra.

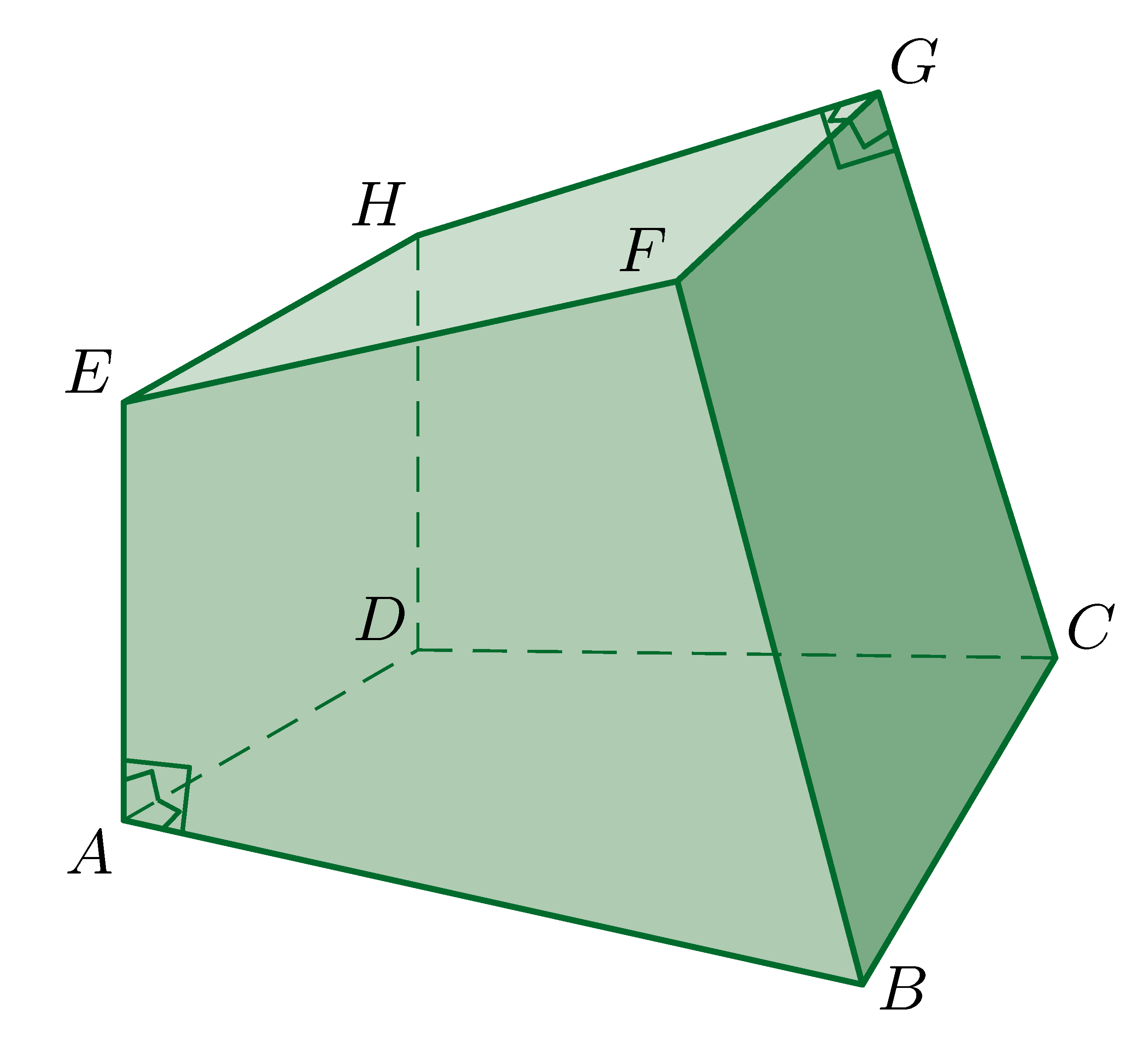
Igazoljuk, hogy

$\displaystyle [ABCD]^2+[ABFE]^2+[ADHE]^2 = [BCGF]^2+[CDHG]^2+[EFGH]^2.$

($\displaystyle [XYZW]$ az $\displaystyle XYZW$ négyszög területét jelöli.)

Javasolta: Kós Géza (Budapest)

(6 pont)

A beküldési határidő 2025. április 10-én LEJÁRT.

Megoldás. A következő jól ismert tételt fogjuk használni: ha egy poliéder minden lapjára merőlegesen kifelé rajzolunk egy vektort, amelynek hossza éppen az adott lap területe, akkor ezen vektorok összege a nullvektor. (Bővebben lásd itt és itt. Az állítás szorosan kapcsolódik a nevezetes, 1897-ből származó Minkowski-problémához (illetve annak a speciális esetéhez), amellyel kapcsolatban Minkowski eredeti cikke itt olvasható.)

Rátérve a feladat megoldására, jelölje tehát a fenti eredménynek megfelelően $\displaystyle \mathbf{t}_{XYZW}$ az $\displaystyle XYZW$ lap kifelé mutató normálvektorát, amelynek hossza éppen $\displaystyle XYZW$ lap területe. Ekkor a tétel szerint

$\displaystyle \mathbf{t}_{ABCD} +\mathbf{t}_{ABFE} +\mathbf{t}_{ADHE} +\mathbf{t}_{BCGF} +\mathbf{t}_{CDHG} +\mathbf{t}_{EFGH} = \mathbf{0}.$

Mivel az $\displaystyle A$ csúcsra illeszkedő élek páronként merőlegesek, így a rá illeszkedő lapok is páronként merőlegesek, vagyis $\displaystyle \mathbf{t}_{ABCD}$, $\displaystyle \mathbf{t}_{ABFE}$ és $\displaystyle \mathbf{t}_{ADHE}$ normálvektoraik is páronként merőlegesek. Merőleges vektorok skalárszorzata $\displaystyle 0$, ezért

$\displaystyle \Big (\mathbf{t}_{ABCD} +\mathbf{t}_{ABFE} +\mathbf{t}_{ADHE} \Big )^2=\mathbf{t}^2_{ABCD} +\mathbf{t}^2_{ABFE} +\mathbf{t}^2_{ADHE}+2\mathbf{t}_{ABCD}\mathbf{t}_{ABFE} +2\mathbf{t}_{ABCD} \mathbf{t}_{ADHE}+2 \mathbf{t}_{ABFE}\mathbf{t}_{ADHE}= \mathbf{t}^2_{ABCD} +\mathbf{t}^2_{ABFE} +\mathbf{t}^2_{ADHE}.$

Ugyanígy

$\displaystyle \Big(\mathbf{t}_{BCGF} +\mathbf{t}_{CDHG} +\mathbf{t}_{EFGH}\Big)^2=\mathbf{t}^2_{BCGF} +\mathbf{t}^2_{CDHG} +\mathbf{t}^2_{EFGH}.$

Ezekből az állítás következik, ugyanis

$\displaystyle [ABCD]^2+[ABFE]^2+[ADHE]^2= \mathbf{t}^2_{ABCD} +\mathbf{t}^2_{ABFE} +\mathbf{t}^2_{ADHE} = \Big(\mathbf{t}_{ABCD}+\mathbf{t}_{ABFE}+\mathbf{t}_{ADHE}\Big)^2 =$

$\displaystyle = \Big(-\mathbf{t}_{BCGF}-\mathbf{t}_{CDHG}-\mathbf{t}_{EFGH}\Big)^2=\mathbf{t}^2_{BCGF} +\mathbf{t}^2_{CDHG} +\mathbf{t}^2_{EFGH} = [BCGF]^2+[CDHG]^2+[EFGH]^2.$

Statisztika:

3 dolgozat érkezett.
6 pontot kapott:	Aravin Peter, Gyenes Károly.
5 pontot kapott:	Kámán-Gausz Péter.

A KöMaL 2025. márciusi matematika feladatai