A C. 1054. feladat (2010. november)

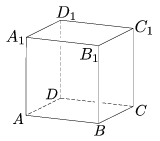
C. 1054. Az ABCDA₁B₁C₁D₁ egységnyi élű kocka BC élnek felezőpontja F, a DCC₁D₁ négyzet középpontja O. Az AFO háromszög síkja két testre vágja szét a kockát. Határozzuk meg e két test térfogatának arányát.

(5 pont)

A beküldési határidő 2010. december 10-én LEJÁRT.

Megoldás. Jelöljük $\displaystyle AFO$ síkját $\displaystyle S$-sel. Határozzuk meg $\displaystyle S$ és a $\displaystyle CC_1D_1D$ lap metszésvonalát. Az $\displaystyle e(AF)$ egyenes az $\displaystyle ABCD$ lap síkjának egyenese, ezért a $\displaystyle CC_1D_1D$ lap síkját olyan pontban metszi, ami mindkét síknak pontja, azaz a $\displaystyle e(CD)$ él egyenesén. Legyen ez a pont $\displaystyle E$. $\displaystyle ABF\triangle \cong ECF\triangle$, mert egymás tükörképeik $\displaystyle F$-re (v. megfelelő szögek csúcs szögek ill. derékszög, és a megfelelő befogó 1/2 hosszú), ezért $\displaystyle CE=1$ és $\displaystyle E$ pont rajta van a metsző $\displaystyle S$ síkon. A feladat szerint $\displaystyle O$ is $\displaystyle S$-en van, ezért $\displaystyle e(OE)$ egyenes is $\displaystyle S$ része. Ezen egyenes metszéspontjai $\displaystyle CC_1$ és $\displaystyle DD_1$ szakaszokkal legyenek rendre $\displaystyle G$ és $\displaystyle H$. Párhuzamos szelőszakaszok tételét alkalmazva ($\displaystyle CC_1$ és $\displaystyle DD_1$ párhuzamosságából következik $\displaystyle DH$ és $\displaystyle CG$ párhuzamossága), felhasználva $\displaystyle OT=1/2$ és $\displaystyle TE=3/2$-t kapjuk, hogy $\displaystyle CG=1/3$ és $\displaystyle DH=2/3$. Másrészről $\displaystyle S$ pontjai voltak $\displaystyle F$ és $\displaystyle G$ a $\displaystyle BCC_1B_1$ lapon, tehát ezt a lapot $\displaystyle FG$ szakaszban metszi $\displaystyle S$, ugyanígy $\displaystyle ADD_1A_1$ lapot $\displaystyle AH$ szakaszban metszi $\displaystyle S$. Az egyik test tehát az $\displaystyle ADHFCG$ lesz, melynek $\displaystyle ADH$ és $\displaystyle FCG$ lapjai párhuzamosak. Továbbá ezt a testet megkaptuk úgy is, mint az $\displaystyle ADHE$ tetraédernek az egységkockánkba eső része (azaz a szóban forgó test egy csonkagúla). $\displaystyle V_{ADHFCG}=V_{ADHE}-V_{FCGE}=\displaystyle{\frac 13 \left(\frac{1\cdot \frac 23}{2}\cdot 2\right)-\frac 13 \left(\frac{\frac 12\cdot \frac 13}{2}\cdot 1\right)=\frac 7{36}}$. Az $\displaystyle S$ által meghatározott testek térfogata $\displaystyle \frac 7{36}$ és $\displaystyle 1-\frac 7{36}=\frac{29}{36}$, ezért a két test térfogatának aránya $\displaystyle \frac{7}{29}$.

Statisztika:

102 dolgozat érkezett.
5 pontot kapott:	Barta Szilveszter Marcell, Bingler Arnold, Fonyó Viktória, Gehér Péter, Heimann Gergő, Jenei Márk, Juhász Bálint, Karádi 468 Dániel Tamás, Károly Péter Balázs, Kasó Márton, Leitereg András, Nagy 021 Tibor, Nagy Anna Noémi, Németh Klára Anna, Rácz Viktória, Sagmeister Ádám, Samu Viktor, Schultz Vera Magdolna, Tamás Ádám, Temesvári Fanni, Tóth Balázs, Ványi Richárd Mihály, Végh Dávid András.
4 pontot kapott:	30 versenyző.
3 pontot kapott:	15 versenyző.
2 pontot kapott:	9 versenyző.
1 pontot kapott:	4 versenyző.
0 pontot kapott:	16 versenyző.
Nem versenyszerű:	5 dolgozat.

A KöMaL 2010. novemberi matematika feladatai