A C. 1074. feladat (2011. március)

C. 1074. Az egység élű kocka AB éle milyen messze van az EC testátlótól?

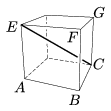
(5 pont)

A beküldési határidő 2011. április 11-én LEJÁRT.

Megoldás. Két kitérő egyenes távolsága nem más, mint a rájuk illeszkedő, egymással párhuzamos síkok távolsága. Ezt megkaphatjuk úgy, hogy az egyik síkra állítunk egy merőleges síkot, hogy a metszésvonaluk az adott egyenes legyen. Ez a merőleges sík a másik egyenest metszi (mert nem lehet párhuzamos vele). A metszésponton átmenő, az első egyenesre merőleges egyenes mindkét egyenesre és mindkét - a rájuk fektetett, egymással párhuzamos - síkra is merőleges: a metszéspontok által meghatározott szakasz hossza lesz a két egyenes távolsága.

Megmutatjuk, hogy az $\displaystyle AB$ él $\displaystyle M$ felezőpontja és a $\displaystyle CE$ testátló $\displaystyle N$ felezőpontja által meghatározott szakasz merőleges mind $\displaystyle AB$-re, mind $\displaystyle CE$-re, ezért ezen szakasz hossza lesz a keresett távolság. $\displaystyle N$ a kocka középpontja, $\displaystyle M$ tükörképe $\displaystyle N$-re pont a $\displaystyle GH$ él felezőpontja, $\displaystyle M'$. Mivel $\displaystyle MM'GB$ paralelogramma ($\displaystyle MB$ párhuzamos és egyenlő hosszú $\displaystyle M'G$-vel), ezért $\displaystyle MN=\frac{\sqrt 2}{2}$. Mivel $\displaystyle MN$ benne van az $\displaystyle AB$ felező merőleges síkjában, ezért $\displaystyle MN$ merőleges $\displaystyle AB$-re. Másrészről $\displaystyle FC=\frac{\sqrt3}2$, mert a testátló fele, ezért Pithagorsz tétel megfordítását alkalmazva $\displaystyle MN^2+FC^2=\frac12 + \frac34=\frac54$ és $\displaystyle MC$, az $\displaystyle MBC$ derékszögű háromszög átfogója, tehát (Pithagorasz tétellel) $\displaystyle MC^2=MB^2+BC^2=\frac 14 + 1=\frac54$, azaz $\displaystyle MN^2+FC^2=MC^2$: $\displaystyle MN$ merőleges $\displaystyle EC$-re. A keresett távolság tehát $\displaystyle MN=\frac{\sqrt 2}{2}$.

Statisztika:

133 dolgozat érkezett.
5 pontot kapott:	88 versenyző.
4 pontot kapott:	11 versenyző.
2 pontot kapott:	15 versenyző.
1 pontot kapott:	7 versenyző.
0 pontot kapott:	7 versenyző.
Nem versenyszerű:	5 dolgozat.

A KöMaL 2011. márciusi matematika feladatai