A C. 1079. feladat (2011. április)

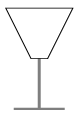
C. 1079. Pezsgőspoharunk csonkakúp alakú, az alapkör sugara 1 cm, a fedőkör sugara 4 cm, a magassága 6 cm (lásd az ábrát). Milyen magasságig kell tölteni a poharat, ha egy fél pohár italt szeretnénk inni?

(5 pont)

A beküldési határidő 2011. május 10-én LEJÁRT.

Megoldás. Egészítsük ki a poharat adó csonkakúpot kúppá, ennek keresztmetszete látható az ábrán. A csonkakúpot kúppá egy olyan kúppal egészítettük ki, mely alapkörének sugara 1cm, magassága $\displaystyle x$, térfogatát jelöljük $\displaystyle V_1$-gyel. Töltsük $\displaystyle m$ magasságig a poharat pezsgővel. A kiegészítő kúp és a poharat tartalmazó kúp hasonlóak, a hasonlóság aránya 1:4, így a magasságaikra $\displaystyle x:(6+x)=1:4$, ahonnan $\displaystyle x=2$(cm); a pezsgővel töltött pohárrészre a (kúpok) hasonlóságból pedig $\displaystyle r:1=(m+2):2$. A pohár űrtartalma $\displaystyle V_0=\frac 13 \pi(4^2\cdot 8-1^2 \cdot 2)=42\pi (cm^3)$. A feladat szerint $\displaystyle 21\pi (cm^3)$ pezsgőt töltöttünk: $\displaystyle 21\pi (cm^3)=\frac 13 \pi \left((\frac{m+2}2)^2 \cdot (m+2) -1^2 \cdot 2\right)$, ahonnan $\displaystyle m\approx 4,38$(cm).

Statisztika:

135 dolgozat érkezett.
5 pontot kapott:	78 versenyző.
4 pontot kapott:	25 versenyző.
3 pontot kapott:	7 versenyző.
2 pontot kapott:	17 versenyző.
1 pontot kapott:	6 versenyző.
0 pontot kapott:	1 versenyző.
Nem versenyszerű:	1 dolgozat.

A KöMaL 2011. áprilisi matematika feladatai