A C. 1293. feladat (2015. április)

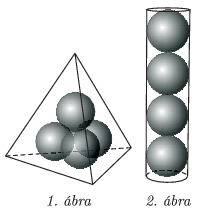
C. 1293. Az Alfa sportszergyártó négyesével csomagolja a teniszlabdákat: gúlába rendezve egy szabályos tetraéder alakú dobozba (1. ábra). Az AFLA cég szintén négyesével csomagolja a teniszlabdákat: egymásra téve egy hosszú henger alakú (alul-felül zárt) dobozba (2. ábra). Mekkora az eltérés a kétféle doboz felülete között, ha egy teniszlabda átmérője 6,50 cm?

(5 pont)

A beküldési határidő 2015. május 11-én LEJÁRT.

Megoldás. Az AFLA cég esetében a henger alakú doboz alaplapjának sugara 3,25 cm, magassága pedig \(\displaystyle 4\cdot6,5=26\) cm, így felülete \(\displaystyle 2\cdot 3,25^2\pi+6,5\pi\cdot26\approx597,30\rm{~cm}^2\).

Az Afla cég esetében észrevehető, hogy a teniszlabdák, mint gömbök középpontjai által meghatározott szabályos tetraéder hasonló a szabályos tetraéder alakú dobozhoz. Mivel a labdák érintik egymást, ezért a kis tetraéder éle \(\displaystyle a=6,5\) cm. A nagy tetraédert jelölje \(\displaystyle T\), a kicsit \(\displaystyle t\). Az érintés miatt \(\displaystyle t\) csúcsai \(\displaystyle T\) megfelelő lapjaitól \(\displaystyle 3,25\) cm távolságra vannak. \(\displaystyle T\) és \(\displaystyle t\) súlypontja egybeesik, célszerű lenne a súlypont helyzetét meghatározni, mert ebből kiszámítható lenne \(\displaystyle T\) éle.

Mivel \(\displaystyle t\) alaplapja szabályos háromszög, aminek magassága \(\displaystyle m=\frac{\sqrt3}{2}\cdot6,5\), így \(\displaystyle t\) magasságának (ami egyben a súlyvonala is) hossza a Pitagorasz-tétel szerint

\(\displaystyle \sqrt{6,5^2-\left(\frac {2m}{3}\right)^2}=\sqrt{6,5^2-\frac13\cdot6,5^2}=\sqrt{\frac23}\cdot6,5.\)

Mivel a súlypont a súlyvonal laphoz közelebbi negyedelő pontja, ezért \(\displaystyle t\) lapjaitól \(\displaystyle \frac14\cdot\sqrt{\frac23}\cdot6,5=\sqrt{\frac23}\cdot1,625\) távolságra van. Ebből következik, hogy \(\displaystyle T\) lapjaitól a súlypont \(\displaystyle \sqrt{\frac23}\cdot1,625+3,25\) távolságra van.

Tehát \(\displaystyle T\) és \(\displaystyle t\) hasonlóságának aránya

\(\displaystyle \frac{\sqrt{\frac23}\cdot1,625+3,25}{\sqrt{\frac23}\cdot1,625}= \frac{\sqrt{\frac23}+2}{\sqrt{\frac23}}=1+\sqrt6.\)

Tehát \(\displaystyle T\) éle \(\displaystyle b=(1+\sqrt6)\cdot6,5\), felülete pedig

\(\displaystyle 4\cdot \frac{\sqrt{3}}{4}b^2=\sqrt3\cdot\left((1+\sqrt6)\cdot6,5\right)^2\approx870,76\rm{~cm}^2.\)

A két felület közötti eltérés \(\displaystyle 870,76-597,30=273,46\rm{~cm}^2\).

Statisztika:

31 dolgozat érkezett.
5 pontot kapott:	Egyházi Anna, Fehér Balázs, Fényes Balázs, Fülöp Erik, Kasó Ferenc, Mándoki Sára, Sándor Gergely, Sudár Ákos, Telek Máté László, Török Réka , Varjas István Péter, Vida Máté Gergely.
4 pontot kapott:	Bereczki Zoltán, Bodonhelyi Anna, Bottlik Judit, Erdei Ákos, Farkas Dóra, Juhász 333 Katalin, Kósa Szilárd, Krisztián Jonatán, Matusek Márton, Mátyus Adrienn, Mészáros 01 Viktória, Pap-Takács Mónika, Szűcs Dorina, Tóth Bence Tamás.
3 pontot kapott:	1 versenyző.
2 pontot kapott:	3 versenyző.
1 pontot kapott:	1 versenyző.

A KöMaL 2015. áprilisi matematika feladatai