A C. 1371. feladat (2016. október)

C. 1371. Egy egységnyi oldalú négyzet oldalait osszuk fel \(\displaystyle n\)–\(\displaystyle n\) egyenlő részre, és a szemközti oldalak osztópontjait eggyel elcsúsztatva kössük össze egymással az ábrán látható módon (az ábra az \(\displaystyle n=5\) esetet ábrázolja). Bizonyítsuk be, hogy a keletkező darabokból \(\displaystyle n^2+1\) egybevágó kisebb négyzetet lehet összerakni.

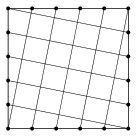
(5 pont)

A beküldési határidő 2016. november 10-én LEJÁRT.

Megoldás. Az 1. ábra jelöléseit használva, toljuk el az \(\displaystyle ABE\) háromszöget \(\displaystyle \overrightarrow{BC}\) vektorral, így kapjuk a \(\displaystyle CDG\) háromszöget; majd a \(\displaystyle BCF\) háromszöget \(\displaystyle \overrightarrow{BA}\) vektorral, így az \(\displaystyle ADH\) háromszöghöz jutunk. Ezzel átdaraboltuk az eredeti \(\displaystyle ABCD\) négyzet területét az \(\displaystyle AEFCGH\) sokszögbe.

1. ábra

A 2. ábra jelöléseit használva, legyen az \(\displaystyle FE\) és a \(\displaystyle GH\) egyenes metszéspontja \(\displaystyle K\). Ekkor az \(\displaystyle FCGK\) négyszög négyzet, ami \(\displaystyle n^2\) kisebb négyzetből áll és ezekkel egybevágó az \(\displaystyle AEKH\) kis négyzet.

Ezzel beláttuk, hogy az eredeti \(\displaystyle ABCD\) négyzet átdarabolásával \(\displaystyle n^2+1\) kisebb négyzetet lehet összerakni.

Statisztika:

195 dolgozat érkezett.
5 pontot kapott:	146 versenyző.
4 pontot kapott:	36 versenyző.
3 pontot kapott:	8 versenyző.
2 pontot kapott:	3 versenyző.
1 pontot kapott:	1 versenyző.
0 pontot kapott:	1 versenyző.

A KöMaL 2016. októberi matematika feladatai