 |
A C. 1408. feladat (2017. március) |
C. 1408. Tegyünk le az asztalra nyolc különböző dominót a játék szabályai alapján úgy, hogy egy zárt négyzetet alkossanak (az ábrán egy ilyen elrendezés látható). Mennyi lehet a dominókon lévő pontok összegének legkisebb és legnagyobb értéke?
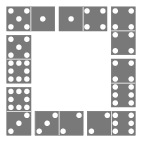
(5 pont)
A beküldési határidő 2017. április 10-én LEJÁRT.
Megjegyzés. Legjobb szándékunk ellenére sem lett teljesen egyértelmű a feladat. Mi két készletet ismertünk: a 0-tól 6-ig és a 0-tól 9-ig pöttyözöttet. Az ábrával kizártuk azt a dominókészletet, amiben 0-tól 6-ig szerepelnek a pöttyök, ám van ezeken kívül másmilyen is, amiben ilyen dominók szerepelhetnek. A megoldásból látni lehet, hogy ez csak a maximális értéknél számít, itt elfogadjuk a 6-oson kívül bármelyik létező készletet.
Megoldás. A pontok helyett számokat írunk a dominókra, így egyszerűbb a leírás.
Először keressük meg a legkisebb értéket. Írjuk fel egy táblázatba a dominók legkisebb értékeit:

Minden dominó mindkét oldala egy-egy másikkal érintkezik, mindegyiknek van párja, így minden felhasznált szám páros sokszor fordul elő a 8 dominón, azaz 16 oldalon.
Vegyük sorba az eseteket aszerint, hogy hány dominó tartalmaz 0 számot.
a) Ha van 6 olyan dominó, amely tartalmaz 0-t, ezek között nem szerepelhet a 0-0 dominó, mert akkor páratlan lenne a 0-k száma. Így a 0-1, 0-2, 0-3, 0-4, 0-5, 0-6 dominókról van szó. Ekkor a maradék két dominón lévő 4 hely nem elég ahhoz, hogy minden szám kétszer szerepeljen.
b) Ha 5 dominó tartalmaz 0-t, akkor a páros darabszám miatt a 0-0 dominó is köztük van. Az 5 legkisebb ilyen dominó: 0-0, 0-1, 0-2, 0-3, 0-4. Ezekhez biztosan szükséges egy-egy az 1, 2, 3, 4 számokból, ez két dominót jelent. A maradék egy dominó legkisebb lehetséges értéke a táblázat alapján az 1-1.
Tehát ekkor az összeg minimum: (1+2+3+4)⋅2+1+1=22.
c) Ha 4 dominó tartalmaz 0-t, akkor a páros darabszám miatt a 0-0 nem lehet köztük. Így a legkisebb összeg a 0-1, 0-2, 0-3, 0-4 esetben lesz. Ekkor, hasonlóan az előző esethez, szintén kell még egy-egy az 1, 2, 3, 4-es számokból, két dominón. A maradék két dominó a b) esetben 0-0 és az 1-1 voltak. Itt most a 0-0 nem szerepelhet, így a minimum összeg biztosan nagyobb lesz 22-nél.
d) Ha 3 dominó tartalmaz 0-t, akkor szerepelnie kell a 0-0 dominónak. A 0-0, 0-1, 0-2 választás a legkedvezőbb. Lesz 5 olyan dominó, amin nem szerepel 0. A táblázat alapján a legkisebb összeghez az 1-1, 1-2, 1-3, 2-2 dominók, illetve az 1-4 és 2-3 dominók közül az egyik kellene. Így az összeg 21 lenne.
Azonban, ha az utolsó dominó az 1-4, akkor a nyolc dominó: 0-0, 0-1, 0-2, 1-1, 1-2, 1-3, 2-2, 1-4, és ekkor csak 1 db 4-es és 1 db 3-as van.
Ha az utolsó dominó a 2-3, akkor a nyolc dominó: 0-0, 0-1, 0-2, 1-1, 1-2, 1-3, 2-2, 2-3. Ekkor 5 db 2-es van, ez sem páros, nem lehetséges.
Így legalább egy dominót mindkét esetben ki kell cserélni, aminek következtében az összeg nőni fog, nem lehet 21, minimum 22 lesz.
e) Hat darab, 0-t nem tartalmazó dominóval a legkisebb elérhető összeg a táblázat szerint 23. Így, ha csak 2, 1 vagy 0 db dominó tartalmaz 0 számot, akkor az összeg biztosan nagyobb lesz 22-nél.
Az összes esetre beláttuk, hogy az összeg minimum 22 pötty lehet, erre egy példa:

A maximum érték 9 pötty esetén: A maximális érték úgy is kiszámolható, hogy az előző példában minden x számot kicserélünk (9−x)-re. Tehát a maximális érték: 16⋅9−22=122 pötty. Erre egy példa:

A maximum érték 8 pötty esetén: A maximális érték úgy is kiszámolható, hogy az előző példában minden x számot kicserélünk (8−x)-re. Tehát a maximális érték: 16⋅8−22=106 pötty.
Erre egy példa:

A többi dominókészlet esetén is hasonlóan adható meg a pöttyök számának maximuma.
Vida Tamás (Győr, Kazinczy F. Gimn., 9. évf.) dolgozata alapján
Statisztika:
172 dolgozat érkezett. 5 pontot kapott: 81 versenyző. 4 pontot kapott: 5 versenyző. 3 pontot kapott: 5 versenyző. 2 pontot kapott: 24 versenyző. 1 pontot kapott: 5 versenyző. 0 pontot kapott: 43 versenyző. Nem versenyszerű: 9 dolgozat.
A KöMaL 2017. márciusi matematika feladatai
|
|

