A C. 1449. feladat (2017. december)

C. 1449. Egy egységsugarú körbe szabályos nyolcágú csillagot írtunk az ábrán látható módon. Mekkora a csillag kerülete?

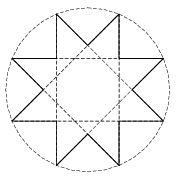
(5 pont)

A beküldési határidő 2018. január 10-én LEJÁRT.

1. megoldás. Használjuk az ábra jelöléseit.

A kör sugara egységnyi, így az \(\displaystyle ACO\) derékszögű háromszögben \(\displaystyle AC=a=\sqrt2\). Az \(\displaystyle ACF\) háromszögben \(\displaystyle FB\) szögfelező, így a \(\displaystyle CLF\) derékszögű háromszögben:

\(\displaystyle \frac a2=FC\cdot \sin 22,5°.\)

Tehát \(\displaystyle FC=\frac{a}{2\sin 22,5°}=\frac{\sqrt2}{2\sin 22,5°}\).

Az \(\displaystyle OED\) háromszögben hasonló gondolatmenettel:

\(\displaystyle \frac d2=OE\sin 22,5°=\sin 22,5°,\)

\(\displaystyle d=2\sin 22,5°.\)

A \(\displaystyle DEJK\) négyszög téglalap, így \(\displaystyle JK=d=2\sin 22,5°\), így

\(\displaystyle FJ+KC=2x=FC-JK=\frac{\sqrt2}{2\sin 22,5°}-2\sin 22,5°≈1,08239.\)

A nyolcágú csillag kerülete:

\(\displaystyle K=16x=8\cdot 2x≈8,65914.\)

Megjegyzés. Ha a \(\displaystyle \sin 22,5°\) pontos értékével, \(\displaystyle \frac{\sqrt{2-\sqrt2}}{2}\)-vel számolunk, akkor a végeredmény \(\displaystyle 8\left(\sqrt{2+\sqrt2}-\sqrt{2-\sqrt2}\right)\).

1. megoldás. Szögfüggvények nélkül is ki lehet számolni a kérdéses kerületet. Az alábbi megoldást Horváth Antal, Szeged, SZTE Juhász Gyula Gyak. Ált. Isk., 8. oszályos tanulója adta:

C1449.pdf

Statisztika:

96 dolgozat érkezett.
5 pontot kapott:	Abonyi Kata, Babolcsay Barbara, Baráth Bettina, Baráth László, Biró 424 Ádám, Bottlik Domonkos, Csécsi Marcell, Czett Mátyás, Debreczeni Dorina, Fazekas 5 Zsófia, Fonyi Máté Sándor, Forgács Kata, Földvári Ádám, Gém Viktória, Halász 237 Lajos, Hordós Adél Zita, Horváth Antal, Jánosdeák Márk, Jávorka Marcell, Kalabay László, Kerekes Boldizsár, Kis 194 Károly, Koleszár Domonkos, Kovács 157 Zita, Kovács Fruzsina Dóra, Kozma Kristóf, Leskó Eszter Rózsa, Markó Gábor, Mendei Barna, Nagy 202 Eszter , Országh Júlia, Pálfi Bálint, Papp Márton, Pinke Andrea, Rusvai Miklós, Schenk Anna, Shuborno Das, Szalontai Kinga Sára, Szeibel Richard, Szemerédi Előd, Szőke Péter, Tóth Lilla Eszter , Trombitás Karolina Sarolta, Urszuly Csenge, Veibli-Magyari Kristóf, Werner András, Williams Hajna.
4 pontot kapott:	16 versenyző.
3 pontot kapott:	4 versenyző.
2 pontot kapott:	6 versenyző.
1 pontot kapott:	11 versenyző.
0 pontot kapott:	12 versenyző.

A KöMaL 2017. decemberi matematika feladatai