 |
A C. 1481. feladat (2018. április) |
C. 1481. Egy \(\displaystyle 2\) sugarú körbe írt szabályos nyolcszög csúcsait három különböző módon kötjük össze az ábra szerint: minden szomszédos, minden másodszomszédos, majd minden harmadszomszédos csúcsot. Igazoljuk, hogy a három beírt kör sugarának szorzata \(\displaystyle 2\).
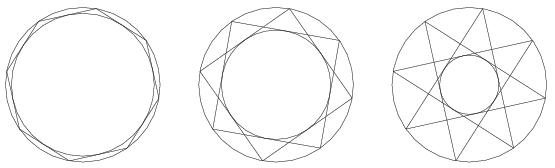
(5 pont)
A beküldési határidő 2018. május 10-én LEJÁRT.
Megoldás. Használjuk az 1. ábra jelöléseit. Az \(\displaystyle OAF\) derékszögű háromszögben
\(\displaystyle α=\frac{AOB∡}{2}=\frac{45°}{2}=22,5°,\)
\(\displaystyle r_1=2\cdot\cos22,5°.\)
1. ábra
A 2. ábrán jól látható, hogy
\(\displaystyle r_3=\frac{AB}{2}=AF=2\cdot\sin22,5°.\)
2. ábra
A 3. ábra alapján az \(\displaystyle OCM\) derékszögű, egyenlő szárú háromszögben
\(\displaystyle r_2=\frac{2}{\sqrt2}=\sqrt2.\)
3. ábra
A három sugár szorzata:
\(\displaystyle r_1\cdot r_2\cdot r_3=2\sqrt2\cdot 2\cos22,5°\cdot \sin22,5°=2\sqrt2\sin45°=\frac{2\sqrt2}{\sqrt2}=2.\)
Megjegyzés. A pontlevonások szinte mindegyike hiányos indoklásból adódott. Jellemzően a szögek nagyságát nem indokolták egyes versenyzők, de olyanok is voltak, akik közelítő értékkel számoltak, számolási hibát vétettek, vagy a képleten túl semmilyen indoklást nem nyújtottak.
Statisztika:
31 dolgozat érkezett. 5 pontot kapott: Agócs Katinka, Ajtai Boglárka, Bukor Benedek, Dobay Ádám, Jankovits András, Magyar 257 Boglárka, Molnár 410 István, Németh Csilla Márta, Spányik Teodor, Surján Anett, Szécsi Adél Lilla. 4 pontot kapott: Almási Adél Csilla, Debreczeni Tibor, Dékány Barnabás, Gálffy Veronika, Kis-Tóth Janka, Kiszelovics Dorina, Kovács 161 Márton Soma, Nyitrai Boglárka, Paksi Barnabás, Rittgasszer Ákos, Sal Dávid, Szőnyi Laura, Vlaszov Artúr. 3 pontot kapott: 6 versenyző. 2 pontot kapott: 1 versenyző.
A KöMaL 2018. áprilisi matematika feladatai