A C. 1496. feladat (2018. szeptember)

C. 1496. Egy háromszög csúcsai körül vett 1, 2, illetve 3 cm sugarú körök páronként kívülről érintik egymást. Mekkora területet nem fednek le a körök a háromszögből?

(5 pont)

A beküldési határidő 2018. október 10-én LEJÁRT.

Megoldás. Ha két kör érinti egymást, akkor az érintési pont a körök középpontját összekötő szakaszon van. Vagyis az érintési pontok az oldalakon helyezkednek el. Használjuk az ábra jelöléseit.

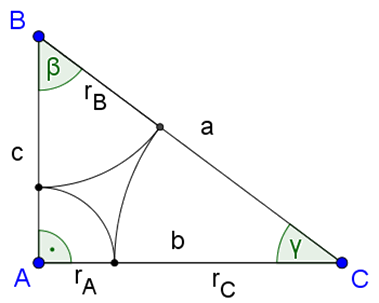
A körök sugarai: \(\displaystyle r_A=1\) cm, \(\displaystyle r_B=2\) cm, \(\displaystyle r_C=3\) cm. A háromszög oldalai tehát: \(\displaystyle a=2+3=5\) cm, \(\displaystyle b=1+3=4\) cm, \(\displaystyle c=1+2=3\) cm. A háromszög derékszögű, mivel \(\displaystyle 5^2=4^2+3^2\).

\(\displaystyle \sin β=4/5\), amiből \(\displaystyle β≈53,13°\), és így \(\displaystyle \gamma=90^{\circ}-\beta=36,87°\).

A körcikkek területe: \(\displaystyle T_A=\frac{π\cdot r_A^2}4=\frac π4≈0,7854\) cm\(\displaystyle ^2\), \(\displaystyle T_B=\frac{π\cdot r_B^2\cdot 53,13°}{360°}≈1,8546\) cm\(\displaystyle ^2\), \(\displaystyle T_C=\frac{π\cdot r_C^2\cdot 36,87°}{360°}≈2,8958\) cm\(\displaystyle ^2\). A háromszög területe: \(\displaystyle T_ABC=\frac{bc}2=6\) cm\(\displaystyle ^2\).

A keresett terület: \(\displaystyle T=T_ABC-T_A-T_B-T_C≈0,4642\) cm\(\displaystyle ^2\).

Statisztika:

114 dolgozat érkezett.
5 pontot kapott:	57 versenyző.
4 pontot kapott:	23 versenyző.
3 pontot kapott:	18 versenyző.
2 pontot kapott:	4 versenyző.
1 pontot kapott:	1 versenyző.
0 pontot kapott:	2 versenyző.
Nem számítjuk a versenybe a születési dátum vagy a szülői nyilatkozat hiánya miatt:	9 dolgozat.

A KöMaL 2018. szeptemberi matematika feladatai