A C. 1574. feladat (2019. december)

C. 1574. Az ábrán látható metszéspontokra ráírtunk minden egész számot $\displaystyle 0$-tól $\displaystyle 10$-ig. Ezt követően minden kis háromszögbe beírjuk a csúcsain található számok összegét. Mekkora az így kapott $\displaystyle 14$ szám összegének lehető legnagyobb, illetve legkisebb értéke?

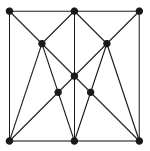
(5 pont)

A beküldési határidő 2020. január 10-én LEJÁRT.

Megoldás. Először nézzük meg, hogy egy-egy metszéspont hány háromszögnek a csúcsa, azaz hány háromszöghöz tartozó összegben fog szerepelni. Ez alapján 5-féle metszéspont található az ábrán:

• 6 háromszögnek csúcsa: 1 db,
• 5 háromszögnek csúcsa: 2 db,
• 4 háromszögnek csúcsa: 4 db,
• 3 háromszögnek csúcsa: 2 db,
• 2 háromszögnek csúcsa: 2 db.

Ahhoz, hogy a 14 háromszögben szereplő szám összege a lehető legnagyobb legyen, a fenti felsorolást nézve csökkenő sorrendben kell beírnunk a számokat a metszéspontokra: A legnagyobb szám, azaz a 10, kerüljön arra a metszéspontra, ami a legtöbb, vagyis hat összegben szerepel, a 9 és a 8 arra, ami ötben, stb. Ekkor a 14 háromszögben szereplő számok összegét ki lehet úgy számolni, hogy a metszéspontokon szerepelő számokat adjuk össze úgy, hogy mindegyiket annyiszor vesszük, ahány háromszögnek csúcsa:

$\displaystyle 6 \cdot 10 + 5 \cdot (9+8) + 4 \cdot (7+6+5+4) + 3 \cdot (3+2)+ 2 \cdot (1+0)=250.$

A lehető legkisebb összeget pedig pont olyankor kapjuk, amikor a fenti felsorolást tekintve a számokat növekvő sorrendben írjuk fel a metszéspontokra úgy, hogy a legkisebb szám, a 0, kerüljön arra a metszéspontra, ami a legtöbb, vagyis hat háromszögnek csúcsa, az 1 és a 2 arra, ami ötnek stb. Ekkor az összeg ilyen alakban is felírható:

$\displaystyle 6 \cdot 0 + 5 \cdot (1+2) + 4 \cdot (3+4+5+6) + 3 \cdot (7+8)+2 \cdot (9+10)= 170.$

Tehát a 14 háromszögben szereplő szám lehető legnagyobb összege 250, lehető legkisebb pedig 170.

Statisztika:

208 dolgozat érkezett.
5 pontot kapott:	127 versenyző.
4 pontot kapott:	36 versenyző.
3 pontot kapott:	26 versenyző.
2 pontot kapott:	12 versenyző.
1 pontot kapott:	3 versenyző.
0 pontot kapott:	3 versenyző.
Nem számítjuk a versenybe a születési dátum vagy a szülői nyilatkozat hiánya miatt:	1 dolgozat.

A KöMaL 2019. decemberi matematika feladatai