 |
A C. 1715. feladat (2022. április) |
C. 1715. A \(\displaystyle k\) kör belsejébe rajzoltunk egy 8 cm sugarú \(\displaystyle k_1\) kört. Mindkét kört metszi az ábrán látható módon egy 15 cm sugarú \(\displaystyle k_2\) kör. Mekkora \(\displaystyle k\) sugara, ha a \(\displaystyle k\) belsejében, de \(\displaystyle k_1\)-en kívül levő satírozott síkidom területe megegyezik a \(\displaystyle k_2\) belsejében levő satírozott síkidomok területének összegével?
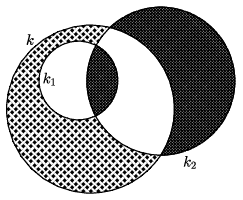
(5 pont)
A beküldési határidő 2022. május 10-én LEJÁRT.
Megoldás. Tekintsük a következő ábrát, amelyen a \(\displaystyle k_1\) és \(\displaystyle k_2\) körök közös részének területét \(\displaystyle T_1\)-gyel, a \(\displaystyle k_2\) kör \(\displaystyle k\) körön kívüli részének területét \(\displaystyle T_2\)-vel, a \(\displaystyle k\) körnek a \(\displaystyle k_1\) és \(\displaystyle k_2\) körökkel nem közös részének területét \(\displaystyle T_3\)-mal jelöltük, végül \(\displaystyle T\)-vel annak a résznek a területét, amely a \(\displaystyle k\) és \(\displaystyle k_2\) körök közös része, de nem tartozik a \(\displaystyle k_1\) körhöz.
A feltétel szerint
| \(\displaystyle (1)\) | \(\displaystyle T_1+T_2=T_3.\) |
Felírhatjuk, hogy \(\displaystyle T+T_1+T_2=15^2\pi\), továbbá a \(\displaystyle k\) kör sugarát \(\displaystyle R\)-rel jelölve \(\displaystyle R^2\pi-8^2\pi-T=T_3\). A két egyenletet összeadva \(\displaystyle T\) értéke kiesik, így azt kapjuk, hogy
| \(\displaystyle (2)\) | \(\displaystyle R^2\pi-8^2\pi+T_1+T_2=T_3+15^2\pi.\) |
A (2) egyenletből (1) alapján az következik, hogy \(\displaystyle R^2\pi=8^2\pi+15^2\pi\), a \(\displaystyle \pi\)-vel való osztás után pedig \(\displaystyle R^2=8^2+15^2=289\), innen pedig \(\displaystyle R=17\), tehát a \(\displaystyle k\) kör sugara 17 cm hosszúságú.
Megjegyzés. A feladatbeli köröket halmazoknak tekintve a \(\displaystyle T_1, T_2, T_3, T\) területeket felírhattuk volna halmazműveletek segítségével is.
Statisztika:
89 dolgozat érkezett. 5 pontot kapott: 71 versenyző. 3 pontot kapott: 4 versenyző. 2 pontot kapott: 2 versenyző. Nem számítjuk a versenybe a születési dátum vagy a szülői nyilatkozat hiánya miatt: 1 dolgozat.
A KöMaL 2022. áprilisi matematika feladatai