A C. 1722. feladat (2022. május)

C. 1722. Az $\displaystyle ABCD$ négyszögről tudjuk, hogy a $\displaystyle AD$ oldal ugyanolyan hosszú, mint a $\displaystyle DC$ oldal, valamint hogy a $\displaystyle DAB$ szöget $\displaystyle \alpha$-val jelölve $\displaystyle ABC\sphericalangle=2\alpha$, $\displaystyle BCD\sphericalangle= 3\alpha$ és $\displaystyle CDA\sphericalangle=4\alpha$. Bizonyítsuk be, hogy az $\displaystyle AB$ oldal kétszer olyan hosszú, mint az $\displaystyle AD$ oldal.

(Német versenyfeladat)

(5 pont)

A beküldési határidő 2022. június 10-én LEJÁRT.

Megoldás. Az $\displaystyle ABCD$ akár konvex, akár konkáv négyszög, belső szögeinek összege $\displaystyle 360^{\circ}$. Ezért a feltétel szerint a belső szögek összege: $\displaystyle \alpha+2\alpha+3\alpha+4\alpha=360^{\circ}$, azaz $\displaystyle 10\alpha=360^{\circ}$, ahonnan

Eszerint a négyszög $\displaystyle A, B, C, D$ csúcsainál levő belső szögek nagysága rendre $\displaystyle 36^{\circ}, 72^{\circ}, 108^{\circ}, 144^{\circ}$, ennek alapján a négyszög konvex.

Tekintsük a következő ábrát.

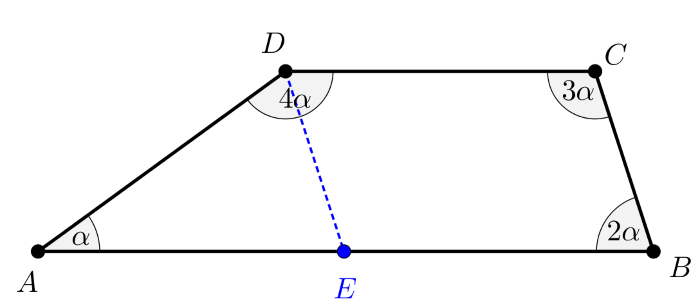
Az (1) eredményből következően $\displaystyle 5\alpha=180^{\circ}$, tehát a négyszög $\displaystyle BC$ és $\displaystyle AD$ oldalán fekvő belső szögek összege mindkét esetben $\displaystyle 180^{\circ}$. Ez pontosan azt jelenti, hogy a négyszög $\displaystyle AB$ és $\displaystyle DC$ oldalai párhuzamosak, vagyis az $\displaystyle ABCD$ négyszög trapéz.

A $\displaystyle D$ ponton átmenő, a $\displaystyle BC$ oldallal párhuzamos egyenes az $\displaystyle AB$ oldalt az $\displaystyle E$ pontban metszi.

Az $\displaystyle AB\parallel{DC}$ miatt nyilvánvaló, hogy $\displaystyle EB\parallel{DC}$ is igaz, továbbá $\displaystyle BC\parallel{ED}$, így $\displaystyle EBCD$ paralelogramma.

Ebből az is következik, hogy $\displaystyle EBC\sphericalangle=CDE\sphericalangle=2\alpha$, valamint $\displaystyle AED\sphericalangle=2\alpha$. Ugyanakkor $\displaystyle CDE\sphericalangle=2\alpha$ miatt $\displaystyle ED$ felezi a $\displaystyle CDA\sphericalangle=4\alpha$ szöget, és így $\displaystyle EDA\sphericalangle=AED\sphericalangle=2\alpha$ is igaz, vagyis $\displaystyle EDA$ egyenlő szárú háromszög. Innen azt kapjuk, hogy $\displaystyle AD=AE$.

Mivel $\displaystyle EBCD$ paralelogramma, ezért $\displaystyle EB=DC$.

Felhasználjuk a feladat azon feltételét, hogy $\displaystyle AD=DC$, ebből $\displaystyle EB=DC$ alapján $\displaystyle EB=AD$, az $\displaystyle AD=AE$ szerint pedig $\displaystyle AE=EB$ következik.

Előző megállapításaink szerint ez azt jelenti, hogy $\displaystyle AB=AE+EB=2AD$, és ezt akartuk bizonyítani.

Statisztika:

60 dolgozat érkezett.
5 pontot kapott:	Ali Richárd, Baksa Anna, Bakurek Máté, Balog Benedek, Baráth Borbála, Beke Botond, Berényi-Sima Lajos, Bettesch Emma Léda, Bettesch Helga Adél, Böröczky András Bálint, Buday Noémi, Dukát Levente, Erdélyi Botond, Fehérvári Donát, Fodor Dóra, Fodor Gergely, Fórizs Emma, Görcsös Ákos Attila, Han Ziying, Hetyei Dániel, Hochenburger Zoárd, Holczer Kenéz, Horváth 221 Zsóka, Inokai Ádám, Iván Máté Domonkos, Juhász Emma, Kerekes András, Kosztolányi Karina, Körmöndi Márk, Laskai Botond, Lipták Bence , Mező Levente, Nagy 292 Korina, Nagy Benedek Márk, Németh Bernát, Petrányi Lilla, Pocsay Levente László, Richlik Márton, Sándor Eszter, Seprődi Barnabás Bendegúz, Somogyi Dóra, Sütő Áron, Szpisják Zsófia Andrea, Tomesz László Gergő, Török Eszter Júlia, Végh Lilian, Vigh 279 Zalán.
4 pontot kapott:	Hetényi Klára Tímea, Rácz Barnabás.

A KöMaL 2022. májusi matematika feladatai