 |
A C. 1758. feladat (2023. március) |
C. 1758. Ádám az egyik rejtvényújságban talált egy bűvös négyzetet (tehát olyan \(\displaystyle 3\times3\)-as számnégyzetet, amelyben az egyes sorokban, oszlopokban, illetve a két átlóban található számok összege megegyezik), melyet ki is töltött helyesen, majd találomra kiválasztott egy sort vagy egy oszlopot a táblázatból, és felírta a benne szereplő számokat balról jobbra vagy fentről lefele olvasva. Ezeket a számokat jelölik az \(\displaystyle a\), \(\displaystyle b\), \(\displaystyle c\) betűk az így keletkező \(\displaystyle ax^2 + bx + c = 0\) egyenletben. Ádám nagy örömmel vette tudomásul, hogy az egyenletnek két valós gyöke is van. Ezek után kiszámolta az egyenlet gyökeinek négyzetösszegét. Milyen számot kaphatott?
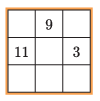
Javasolta: Teleki Olivér (Tököl)
(5 pont)
A beküldési határidő 2023. április 11-én LEJÁRT.
1. megoldás. Először töltsük ki a bűvös négyzetet, jelöljük a középső mezőben lévő számot \(\displaystyle x\)-szel. Ekkor minden sorban, oszlopban és átlóban \(\displaystyle 14+x\) a számok összege, vagyis máris tudjuk, hogy az alsó középső mezőben az \(\displaystyle 5\)-ös áll. Ha a bal alsó mezőben lévő számot \(\displaystyle y\)-nal jelöljük, akkor a jobb felső mezőben a \(\displaystyle 14–y\) áll. Mivel az alsó sorban és a jobb oldali oszlopban azonos a számok összege, ezért \(\displaystyle y+5= (14–y)+3\). Ebből \(\displaystyle 2y=12\), tehát a bal alsó mezőben a \(\displaystyle 6\)-os szám áll. A jobb alsó mezőben ezek szerint \(\displaystyle 3+x\) van, így lesz az alsó sorban is \(\displaystyle 14+x\) a számok összege. Mivel a felső sorban és a bal felső–jobb alsó átlóban is ugyanannyi a számok összege, így \(\displaystyle 9+8=3+2x\). Ebből \(\displaystyle x=7\) – tehát ez van a középső mezőben – és így a bal felső mezőben a \(\displaystyle 4\), a jobb alsóban a \(\displaystyle 10\) áll. Immáron megvan a bűvös négyzet minden eleme:
Még ellenőriznünk kell, hogy tényleg minden sorban és oszlopban ugyanannyi a számok összege, de valóban, mindenütt \(\displaystyle 21\)-et kapunk. A feladatban megadott feltételek alapján Ádám az alábbi \(\displaystyle 6\) másodfokú egyenletet egyikét írta fel:
\(\displaystyle 1)\) \(\displaystyle 4x^2 + 9x + 8 = 0\), amelynek diszkriminánsa \(\displaystyle D_1=9^2-4 \cdot 4 \cdot 8=-47\);
\(\displaystyle 2)\) \(\displaystyle 11x^2 + 7x + 3 = 0\), amelynek diszkriminánsa \(\displaystyle D_2=7^2-4 \cdot 11 \cdot 3=-83\);
\(\displaystyle 3)\) \(\displaystyle 6x^2 + 5x + 10 = 0\), amelynek diszkriminánsa \(\displaystyle D_3=5^2-4 \cdot 6 \cdot 10=-215\);
\(\displaystyle 4)\) \(\displaystyle 4x^2 + 11x + 6 = 0\), amelynek diszkriminánsa \(\displaystyle D_4=11^2-4 \cdot 4 \cdot 6=25\);
\(\displaystyle 5)\) \(\displaystyle 9x^2 + 7x + 5 = 0\), amelynek diszkriminánsa \(\displaystyle D_5=7^2 - 4 \cdot 9 \cdot 5=-131\);
\(\displaystyle 6)\) \(\displaystyle 8x^2 + 3x + 10 = 0\), amelynek diszkriminánsa \(\displaystyle D_6=3^2-4 \cdot 8 \cdot 10=-311\).
Láthatjuk, hogy kizárólag \(\displaystyle D_4 >0\), ezért Ádám biztosan a \(\displaystyle 4\)-es számú egyenletet írta fel. A megoldóképlettel kiszámíthatjuk a két valós gyököt, amelyek \(\displaystyle x_1=-\frac34\) és \(\displaystyle x_2=-2\). A gyökök négyzetösszege
\(\displaystyle x_1^2+x_2^2= (-\frac34)^2+(-2)^2=\frac{73}{16},\)
vagyis ha Ádám helyesen számolt, akkor \(\displaystyle \displaystyle{\frac{73}{16}}\)-ot kapott.
2. megoldás. Jelöljük a bűvös négyzet bal felső sarkában lévő számot \(\displaystyle a\)-val, a jobb felső sarokban lévőt \(\displaystyle b\)-vel, a négyzet közepén lévőt \(\displaystyle c\)-vel, az alsó sorban álló számokat pedig balról jobbra haladva, rendre \(\displaystyle d\)-vel, \(\displaystyle e\)-vel és \(\displaystyle f\)-fel. Mivel az egyes sorokban, oszlopokban és egy-egy átlóban található számok összege megegyezik, ezért speciálisan a középső sorban, illetve oszlopban álló számok összege egyenlő, azaz \(\displaystyle 11+c+3=9+c+e\), amelyből \(\displaystyle e=5\) adódik. Hasonlóképpen az első és harmadik sorban lévő számok összege megegyezik a két átlóban lévők összegével: \(\displaystyle a+9+b+d+5+f=a+c+f+b+c+d,\) ebből \(\displaystyle 2c=14\), vagyis \(\displaystyle c=7\), így az összeg minden esetben \(\displaystyle 21\) kell, hogy legyen.
A négyzet \(\displaystyle 2-2\) sarkában álló számok összegét kiszámíthatjuk a megfelelő sor, oszlop, vagy átló összegéből: \(\displaystyle a+b=21-9=12\), \(\displaystyle a+d=21-11=10\), \(\displaystyle a+f=14\) és \(\displaystyle b+d=14\). Az első két egyenlet megfelelő oldalait összeadva, majd kivonva az utolsó egyenlet megfelelő oldalait, azt kapjuk, hogy \(\displaystyle 2a=8\), amiből \(\displaystyle a=4\). Ezt rendre visszahelyettesítve az első, második és harmadik egyenletbe: \(\displaystyle b=12-4=8\), \(\displaystyle d=10-4=6\) és \(\displaystyle f=14-4=10\).
A fentiek alapján a bűvös négyzet kitöltése egyértelmű, ezért Ádám az alábbi ábrán látható módon töltötte azt ki.
A feladat feltételei alapján Ádám az alábbi \(\displaystyle 6\) másodfokú egyenlet egyikét írta fel:
\(\displaystyle 1)\) \(\displaystyle 4x^2 + 9x + 8 = 0\), amelynek diszkriminánsa \(\displaystyle D_1=9^2-4 \cdot 4 \cdot 8=-47\);
\(\displaystyle 2)\) \(\displaystyle 11x^2 + 7x + 3 = 0\), amelynek diszkriminánsa \(\displaystyle D_2=7^2-4 \cdot 11 \cdot 3=-83\);
\(\displaystyle 3)\) \(\displaystyle 6x^2 + 5x + 10 = 0\), amelynek diszkriminánsa \(\displaystyle D_3=5^2-4 \cdot 6 \cdot 10=-215\);
\(\displaystyle 4)\) \(\displaystyle 4x^2 + 11x + 6 = 0\), amelynek diszkriminánsa \(\displaystyle D_4=11^2-4 \cdot 4 \cdot 6=25\);
\(\displaystyle 5)\) \(\displaystyle 9x^2 + 7x + 5 = 0\), amelynek diszkriminánsa \(\displaystyle D_5=7^2 - 4 \cdot 9 \cdot 5=-131\);
\(\displaystyle 6)\) \(\displaystyle 8x^2 + 3x + 10 = 0\), amelynek diszkriminánsa \(\displaystyle D_6=3^2-4 \cdot 8 \cdot 10=-311\).
Láthatjuk, hogy kizárólag \(\displaystyle D_4 >0\), ezért Ádám biztosan a \(\displaystyle 4\)-es számú egyenletet írta fel. A két különböző valós gyök négyzetösszegének kiszámításakor alkalmazhatjuk a Viéte-formulákat:
\(\displaystyle x_1^2+x_2^2=(x_1+x_2)^2-2x_1x_2=\Big(-\frac{11}{4} \Big)^2-2 \cdot \frac{6}{4}=\frac{73}{16}(=4,\!5625).\)
Ha Ádám helyesen számolt, akkor a \(\displaystyle \displaystyle{\frac{73}{16}}\)-ot kapta a gyökök négyzetösszegeként.
Statisztika:
115 dolgozat érkezett. 5 pontot kapott: 64 versenyző. 4 pontot kapott: 17 versenyző. 3 pontot kapott: 12 versenyző. 2 pontot kapott: 8 versenyző. 1 pontot kapott: 1 versenyző. 0 pontot kapott: 1 versenyző. Nem versenyszerű: 5 dolgozat.
A KöMaL 2023. márciusi matematika feladatai