 |
A C. 1759. feladat (2023. március) |
C. 1759. Egymás mellé helyeztük az \(\displaystyle ABC\) és \(\displaystyle EDC\) derékszögű háromszögeket az ábra szerint.
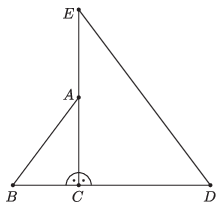
Az \(\displaystyle ABC\) háromszögben \(\displaystyle BC=3\), \(\displaystyle {CA=4}\), az \(\displaystyle EDC\) háromszögben \(\displaystyle DC=6\), \(\displaystyle CE=8\). Az \(\displaystyle ABE\) háromszög körülírt köre a \(\displaystyle DE\) egyenest másodszor a \(\displaystyle P\), a \(\displaystyle DB\) egyenest másodszor a \(\displaystyle Q\) pontban metszi. Határozzuk meg az \(\displaystyle ABDE\) négyszög és az \(\displaystyle AEPQB\) ötszög területe arányának pontos értékét.
Javasolta: Bíró Bálint (Eger)
(5 pont)
A beküldési határidő 2023. április 11-én LEJÁRT.
Megoldás. Az \(\displaystyle ABC\) és \(\displaystyle EDC\) derékszögű háromszögek hasonlók, mert megfelelő befogóik aránya egyenlő:
\(\displaystyle \displaystyle{\frac{BC}{AC}=\frac{DC}{CE}=\frac{3}{4}}.\)
Ezért, ha az \(\displaystyle ABC\) háromszögben \(\displaystyle CAB\sphericalangle=\alpha\), akkor az \(\displaystyle EDC\) háromszögben \(\displaystyle CED\sphericalangle=\alpha\) is igaz.
Tekintsük az alábbi ábrát, amelyen az \(\displaystyle ABE\) háromszög körülírt körét \(\displaystyle k\)-val jelöltük, és megrajzoltuk a \(\displaystyle PB\), illetve \(\displaystyle PQ\) húrokat.
Az ábráról leolvashatjuk, hogy \(\displaystyle EAB\sphericalangle=180^{\circ}-\alpha\), és mivel \(\displaystyle \alpha\) hegyesszög, ezért \(\displaystyle EAB\sphericalangle\) biztosan tompaszög.
Megmutatjuk, hogy a \(\displaystyle P\) és \(\displaystyle Q\) pontok csak az ábrának megfelelően a \(\displaystyle DE\), illetve \(\displaystyle DB\) félegyenesen az \(\displaystyle E\), illetve \(\displaystyle B\) ponton túl helyezkedhetnek el.
A \(\displaystyle P\) pont nem lehet azonos \(\displaystyle E\)-vel, ellenkező esetben a \(\displaystyle DE\) egyenes érintené a \(\displaystyle k\) kört, ami azt eredményezné, hogy \(\displaystyle CED\sphericalangle=\alpha\) érintő szárú kerületi szög lenne, és így a kerületi szögek tétele miatt
\(\displaystyle EBA\sphericalangle=\alpha\)
valósulna meg. Ez azonban lehetetlen, hiszen \(\displaystyle CAB\sphericalangle=\alpha\) külső szöge az \(\displaystyle ABE\) háromszögnek, és így nem állhatna fenn, hogy
\(\displaystyle CAB\sphericalangle=\alpha=EBA\sphericalangle+AEB\sphericalangle.\)
Hasonlóképpen igazolható, hogy a \(\displaystyle Q\) pont nem lehet azonos \(\displaystyle B\)-vel.
Ezután, mivel a \(\displaystyle P\) és \(\displaystyle Q\) pontok illeszkednek a \(\displaystyle k\) körre, ezért ezekből a pontokból az \(\displaystyle EB\) szakasz \(\displaystyle \alpha\) vagy \(\displaystyle 180^{\circ}-\alpha\) szögben látszik. A \(\displaystyle BPE\sphericalangle=180^{\circ}-\alpha\) eset azonban nem fordulhat elő, mert akkor a \(\displaystyle P\) pont a \(\displaystyle k\) körnek a \(\displaystyle B\) és \(\displaystyle E\) pontok által határolt és az \(\displaystyle A\) pontot is tartalmaző körívén lenne, ez pedig lehetetlen, hiszen ennek az ívnek a pontjai a \(\displaystyle B, E\) pontok kivételével a \(\displaystyle BDE\) háromszög belső pontjai. Hasonlóan láthatjuk be, hogy \(\displaystyle BQE\sphericalangle=180^{\circ}-\alpha\) sem lehetséges.
Mindezekből az következik, hogy
| \(\displaystyle (1)\) | \(\displaystyle BPE\sphericalangle=BQE\sphericalangle=\alpha.\) |
(1) szerint \(\displaystyle BPE\sphericalangle=CED\sphericalangle=\alpha\), vagyis \(\displaystyle BP\parallel{CE}\), és így \(\displaystyle BP\) merőleges \(\displaystyle BD\)-re. Az \(\displaystyle EDC\) háromszögben a Pitagorasz-tétel segítségével kapjuk, hogy \(\displaystyle ED=10\). Ezután, mivel \(\displaystyle BP\parallel{CE}\), alkalmazhatjuk a párhuzamos szelők tételét: \(\displaystyle \displaystyle{\frac{PE}{ED}=\frac{BC}{CD}}\), a megfelelő értékek behelyettesítése után \(\displaystyle \displaystyle{\frac{PE}{10}=\frac{3}{6}}\), ahonnan
| \(\displaystyle (2)\) | \(\displaystyle PE=5.\) |
A \(\displaystyle DP\) és \(\displaystyle DQ\) szakaszok a \(\displaystyle k\) körhöz húzott szelők, ezért a szelődarabok szorzatára vonatkozó tétel miatt
\(\displaystyle DE\cdot DP=DB\cdot DQ,\)
ebből a szakaszok hossza, illetve (2) alapján \(\displaystyle 10\cdot 15=9\cdot (9+BQ)\), innen pedig
| \(\displaystyle (3)\) | \(\displaystyle \displaystyle{BQ=\frac{23}{3}}.\) |
A \(\displaystyle PDB\) derékszögű háromszögből \(\displaystyle PD=PE+DE=15\) szerint a Pitagorasz-tételből kapjuk, hogy
| \(\displaystyle (4)\) | \(\displaystyle PB=12.\) |
Az \(\displaystyle ABDE\) négyszög területe az \(\displaystyle ABC\) és \(\displaystyle EDC\) derékszögű háromszögek területének összege (területegységben számolva)
\(\displaystyle \displaystyle{T_{ABDE}=T_{BCA}+T_{DCE}=\frac{3\cdot 4}{2}+\frac{6\cdot 8}{2}=30.}\)
Az \(\displaystyle AEPQB\) ötszög területét a következőképpen számoljuk ki:
\(\displaystyle T_{AEPQB}=T_{PQB}+T_{PDB}-T_{ABDE}.\)
Mivel \(\displaystyle \displaystyle{T_{PQB}=\frac{PB\cdot BQ}{2}}\), ezért (3) és (4) felhasználásával
\(\displaystyle \displaystyle{T_{PQB}=\frac{12\cdot \frac{23}{3} }{2}=46}.\)
A \(\displaystyle PDB\) derékszögű háromszög területe
\(\displaystyle T_{PDB}=\frac{PB\cdot BD}{2}=\frac{12\cdot 9}{2}=54,\)
és tudjuk, hogy \(\displaystyle T_{ABDE}=30\), ezért
\(\displaystyle T_{AEPQB}=46+54-30=70.\)
Ezért az \(\displaystyle ABDE\) négyszög és az \(\displaystyle AEPQB\) ötszög területének aránya:
\(\displaystyle \displaystyle{\frac{T_{ABDE}}{T_{AEPQB}}=\frac{30}{70}=\frac{3}{7}.}\)
Megjegyzés. A (2) eredményhez az \(\displaystyle EDC\) és \(\displaystyle PDB\) derékszögű háromszögek hasonlósága alapján is eljuthatunk.
Statisztika:
A KöMaL 2023. márciusi matematika feladatai