 |
A C. 1799. feladat (2024. február) |
C. 1799. Az egységnyi oldalú \(\displaystyle ABCD\) négyzetben megrajzoltuk a \(\displaystyle DEFG\), \(\displaystyle AHKE\), \(\displaystyle BMFL\) és \(\displaystyle CGNP\) négyzeteket az ábra szerint.
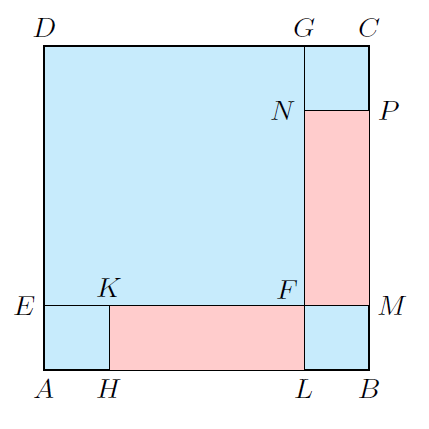
Az \(\displaystyle LFKH\) és \(\displaystyle MPNF\) téglalapok területének összege legfeljebb hányadrésze lehet az \(\displaystyle ABCD\) négyzet területének?
Adjuk meg ebben az esetben az \(\displaystyle \dfrac{ED}{AD}\) arány pontos értékét.
Javasolta: Bíró Bálint (Eger)
(5 pont)
A beküldési határidő 2024. március 11-én LEJÁRT.
Megoldás. Használjuk a feladatban szereplő ábrát és annak jelöléseit a megoldáshoz is!
Legyen \(\displaystyle DE=x\). A \(\displaystyle DEFG\) négyzet, tehát \(\displaystyle DE=DG=x\). Ekkor igazak az alábbi egyenlőségek is:
\(\displaystyle EA=KH=FL=MB=LB=FM=NP=GC=1-x.\)
Az \(\displaystyle LFKH\) és \(\displaystyle MPNF\) téglalapok egybevágók, oldalaik pedig:
\(\displaystyle KH=FM=1-x,\)
\(\displaystyle HL=MP=1-2(1-x)=2x-1.\)
Területösszegüket \(\displaystyle x\) függvényében a következő kifejezések helyettesítési értékei adják meg (ahol \(\displaystyle 0<x<1\)):
\(\displaystyle T_{LFKH}+T_{MPNF}=2(1-x)(2x-1)=2\big(-2x^2+3x-1\big)=-4\Biggl(x^2-\frac{3}{2}x+\frac{1}{2}\Biggr)=-4\Biggl(\Bigl(x-\frac{3}{4}\Bigr)^2-\frac{1}{16}\Biggr)=-4\Biggl(x-\frac{3}{4}\Biggr)^2+\frac{1}{4}.\)
Ennek a kifejezésnek pontosan akkor van maximuma, ha \(\displaystyle \displaystyle{x=\frac{3}{4}}\), ebben az esetben a helyettesítési érték, vagyis a maximális területösszeg \(\displaystyle \displaystyle\frac{1}{4}\). A keresett arány pedig \(\displaystyle \displaystyle{\frac{ED}{AD}=\frac{x}{1}=\frac{3}{4}}\).
Statisztika:
166 dolgozat érkezett. 5 pontot kapott: 93 versenyző. 4 pontot kapott: 32 versenyző. 3 pontot kapott: 7 versenyző. 2 pontot kapott: 6 versenyző. 1 pontot kapott: 4 versenyző. 0 pontot kapott: 2 versenyző. Nem versenyszerű: 5 dolgozat. Nem számítjuk a versenybe a születési dátum vagy a szülői nyilatkozat hiánya miatt: 8 dolgozat.
A KöMaL 2024. februári matematika feladatai