 |
A C. 1809. feladat (2024. április) |
C. 1809. Legyen az \(\displaystyle AC\) szakasz belső pontja \(\displaystyle B\), és az \(\displaystyle ABS_1\), a \(\displaystyle BCS_2\) és az \(\displaystyle CAS_3\) olyan egyenlő szárú háromszögek, amelyek közül semelyik kettőnek nincs közös belső pontja, és amelyeknek alapjai az \(\displaystyle AB\), a \(\displaystyle BC\) és az \(\displaystyle CA\), és az alapon fekvő szögeik mind \(\displaystyle 30^{\circ}\)-osak.
Bizonyítsuk be, hogy az \(\displaystyle S_1S_2S_3\) háromszög szabályos.
német versenyfeladat
(5 pont)
A beküldési határidő 2024. május 10-én LEJÁRT.
Megoldás. Hosszabbítsuk meg a két kisebb háromszög oldalait a következőképp:
- \(\displaystyle AS_3 \cap BS_2 = P\),
- \(\displaystyle CS_3 \cap BS_1 = Q\),
- \(\displaystyle AS_1 \cap CS_2 = R.\)
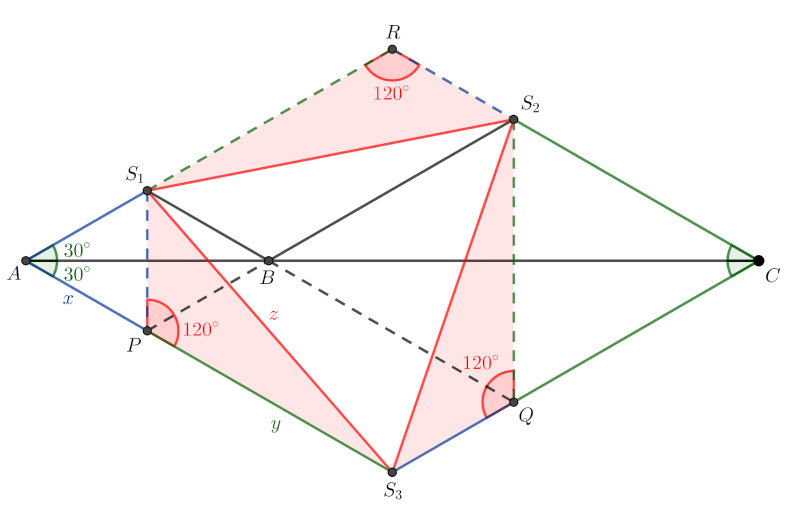
A párhuzamosság miatt a \(\displaystyle PS_{3}QB\), a \(\displaystyle BS_2RS_{1}\) és az \(\displaystyle AS_{3}CR\) négyszögek mindegyike paralelogramma. Ezeknek a tompaszöge mindegyik esetében \(\displaystyle 120^{\circ}\). Továbbá az is igaz, hogy az \(\displaystyle APS_1\) háromszög szabályos, mivel \(\displaystyle AP=AS_1\), és a bezárt szögük \(\displaystyle 60^{\circ}\), ugyanilyen megfontolásból szintén igaz, hogy a \(\displaystyle QCS_2\) is szabályos. Ezek alapján az ábrán pirossal jelölt szögek nagysága
\(\displaystyle S_{1}PS_{3} \sphericalangle = S_3QS_{2} \sphericalangle = S_2RS_{1} \sphericalangle = 120^{\circ}.\)
Mindezekből következően igaz, hogy az alábbi három háromszög egybevágó, ugyanis két oldaluk páronként megegyezik, és az általuk bezárt szög \(\displaystyle 120^{\circ}\):
\(\displaystyle S_1PS_3 \cong S_3QS_2 \cong S_2RS_1.\)
Így \(\displaystyle S_1S_2=S_2S_3=S_3S_1\), tehát az \(\displaystyle S_1S_2S_3\) háromszög valóban szabályos. Ebből adódik a feladatban szereplő szakaszok egyenlősége.
Statisztika:
98 dolgozat érkezett. 5 pontot kapott: 56 versenyző. 4 pontot kapott: 9 versenyző. 3 pontot kapott: 2 versenyző. 2 pontot kapott: 8 versenyző. 1 pontot kapott: 2 versenyző. 0 pontot kapott: 5 versenyző. Nem versenyszerű: 3 dolgozat. Nem számítjuk a versenybe a születési dátum vagy a szülői nyilatkozat hiánya miatt: 7 dolgozat.
A KöMaL 2024. áprilisi matematika feladatai