 Problem C. 1812. (April 2024)
Problem C. 1812. (April 2024)
C. 1812. Let \(\displaystyle a\), \(\displaystyle b\) and \(\displaystyle c\) denote the lengths of the sides of a triangle satisfying \(\displaystyle a+b=3c\). Let \(\displaystyle \alpha\) and \(\displaystyle \beta\) denote the angles opposite to sides \(\displaystyle a\) and \(\displaystyle b\), respectively. Prove that \(\displaystyle \cot{\frac{\alpha}{2}}\cdot{\cot{\frac{\beta}{2}}}=2\).
Croatian competition problem
(5 pont)
Deadline expired on May 10, 2024.
Sorry, the solution is available only in Hungarian. Google translation
1. megoldás. A feladatbeli háromszög létezik, ha az \(\displaystyle a\), \(\displaystyle b\), \(\displaystyle c\) oldalakra teljesül a háromszög-egyenlőtlenség. Ez fennáll, ha a pozitív \(\displaystyle a\), \(\displaystyle b\), \(\displaystyle c\) számokra igaz, hogy
\(\displaystyle a+b>c,\quad a+c>b,\quad b+c>a.\)
Az \(\displaystyle a+b=3c\) feltétel miatt \(\displaystyle a+b>c\) nyilván teljesül, a második egyenlőtlenség pontosan akkor, ha \(\displaystyle a+b+c>2b\), ebből a feltétel alapján \(\displaystyle 2c>b\) következik. A harmadik egyenlőtlenségből hasonlóan adódik, hogy \(\displaystyle 2c>a\) esetben áll fenn.
Ha tehát az \(\displaystyle a\), \(\displaystyle b\), \(\displaystyle c\) pozitív számokra érvényes, hogy
\(\displaystyle 2c>a,\quad 2c>b,\quad a+b=3c,\)
akkor a feladatbeli háromszög létezik. Ilyen számok például
\(\displaystyle a=11,~ b=10, ~c=7;\quad a=9, ~b=6,~ c=5;\quad a=4, ~b=5, ~c=3.\)
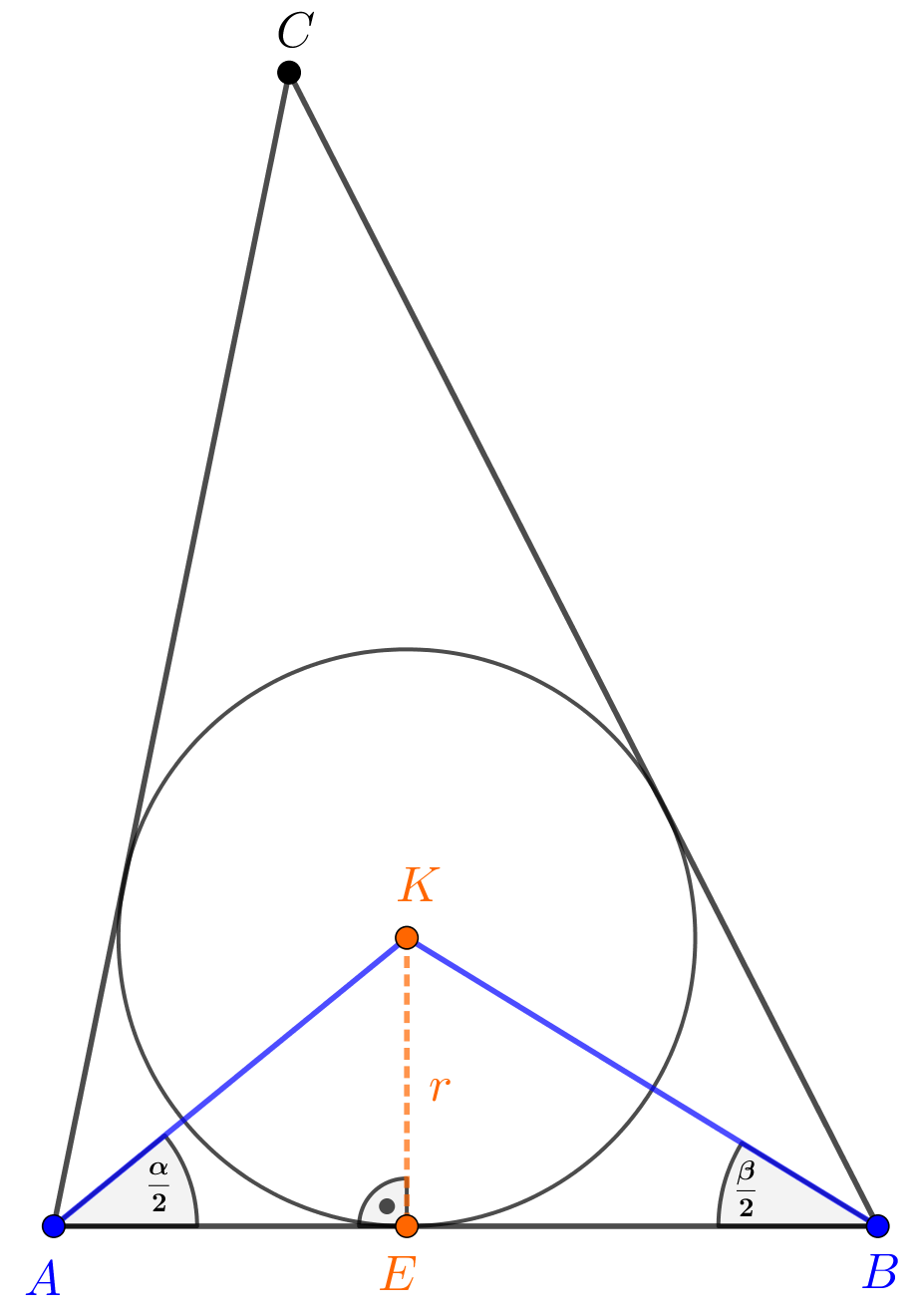
Legyen a feltételeknek megfelelő \(\displaystyle ABC\) háromszög \(\displaystyle r\) sugarú beírt körének középpontja \(\displaystyle K\), a beírt körnek az \(\displaystyle AB\) oldalon levő érintési pontja \(\displaystyle E\).
A háromszög kerülete a feltétel szerint \(\displaystyle a+b+c=4c\), ezért az \(\displaystyle s\) félkerület
| \(\displaystyle (1)\) | \(\displaystyle s=2c.\) |
A háromszög területe kétféleképpen is felírható, a Héron-képlet szerint \(\displaystyle \displaystyle{T=\sqrt{s\cdot(s-a)\cdot(s-b)\cdot(s-c)}},\) a félkerülettel és a beírt kör sugarával \(\displaystyle T=s\cdot r\), ezért
| \(\displaystyle (2)\) | \(\displaystyle \displaystyle{\sqrt{s\cdot(s-a)\cdot(s-b)\cdot(s-c)}=s\cdot r}.\) |
A (2) egyenletből négyzetre emelés és rendezés után azt kapjuk, hogy
| \(\displaystyle (3)\) | \(\displaystyle \displaystyle{\frac{s-a}{r}\cdot\frac{s-b}{r}=\frac{s}{s-c}}.\) |
Ismert, hogy a háromszög \(\displaystyle A\), illetve \(\displaystyle B\) csúcsából a beírt körnek az oldalakon levő érintési pontjaihoz húzott szakaszok hossza \(\displaystyle s-a\), illetve \(\displaystyle s-b\), így az ábrán látható \(\displaystyle AE\), \(\displaystyle BE\) szakaszokra \(\displaystyle AE=s-a,\quad BE=s-b\). Ebből következik, hogy az \(\displaystyle AKE\) és \(\displaystyle BKE\) derékszögű háromszögekben \(\displaystyle \displaystyle{\ctg{\frac{\alpha}{2}}\cdot{\ctg{\frac{\beta}{2}}}=\frac{AE}{r}\cdot\frac{BE}{r}}\), ezért \(\displaystyle \displaystyle{\ctg{\frac{\alpha}{2}}\cdot{\ctg{\frac{\beta}{2}}}=\frac{s-a}{r}\cdot\frac{s-b}{r}}\), ebből pedig (3) alapján
\(\displaystyle \displaystyle{\ctg{\frac{\alpha}{2}}\cdot\ctg{\frac{\beta}{2}}=\frac{s}{s-c}},\)
innen pedig (1) szerint adódik, hogy
\(\displaystyle \displaystyle{\ctg{\frac{\alpha}{2}}\cdot\ctg{\frac{\beta}{2}}=\frac{2c}{c}=2}.\)
2. megoldás. A feltételeknek megfelelő háromszög létezésére vonatkozó megállapításaink azonosak az 1. megoldásban leírtakkal.
Használjuk fel ezután az
\(\displaystyle a=2R\sin\alpha,\quad b=2R\sin\beta,\quad c=2R\sin\gamma\)
összefüggéseket, ahol \(\displaystyle R\) a háromszög körülírt körének sugara. Az \(\displaystyle a+b=3c\) összefüggés alapján ebből adódik, hogy \(\displaystyle \sin\alpha+\sin\beta=3\sin\gamma\), illetve a \(\displaystyle \sin\gamma=\sin(180^{\circ}-\alpha-\beta)=\sin(\alpha+\beta)\) szerint
| \(\displaystyle (4)\) | \(\displaystyle \sin\alpha+\sin\beta=3\sin(\alpha+\beta).\) |
A \(\displaystyle \displaystyle{\sin\alpha+\sin\beta=2\sin\frac{\alpha+\beta}{2}\cdot\cos\frac{\alpha-\beta}{2}}\) és a \(\displaystyle \displaystyle{\sin(\alpha+\beta)=2\sin\frac{\alpha+\beta}{2}\cdot\cos\frac{\alpha+\beta}{2}}\) azonosságok szerint (4)-ből adódik, hogy
\(\displaystyle \displaystyle{2\sin\frac{\alpha+\beta}{2}\cdot\cos\frac{\alpha-\beta}{2}=3\cdot2\sin\frac{\alpha+\beta}{2}\cdot\cos\frac{\alpha+\beta}{2}},\)
ahonnan a \(\displaystyle \displaystyle{2\sin\frac{\alpha+\beta}{2}\neq{0}}\) kifejezéssel osztva kapjuk, hogy \(\displaystyle \displaystyle{\cos\frac{\alpha-\beta}{2}=3\cos\frac{\alpha+\beta}{2}}\), innen pedig átrendezéssel
| \(\displaystyle (5)\) | \(\displaystyle \displaystyle{2\cos\frac{\alpha+\beta}{2}=\cos\frac{\alpha-\beta}{2}-\cos\frac{\alpha+\beta}{2}}.\) |
Az (5) összefüggésben alkalmazzuk az \(\displaystyle \displaystyle{\frac{\alpha}{2}}\), \(\displaystyle \displaystyle{\frac{\beta}{2}}\) szögekre a megfelelő trigonometrikus addíciós tételeket:
\(\displaystyle \displaystyle{2\Bigg(\cos\frac{\alpha}{2}\cdot\cos\frac{\beta}{2}-\sin\frac{\alpha}{2}\cdot\sin\frac{\beta}{2}\Bigg)=2\sin\frac{\alpha}{2}\cdot\sin\frac{\beta}{2}}.\)
Ebből egyszerűsítéssel és rendezéssel kapjuk, hogy
| \(\displaystyle (6)\) | \(\displaystyle \displaystyle{\cos\frac{\alpha}{2}\cdot\cos\frac{\beta}{2}=2\sin\frac{\alpha}{2}\cdot\sin\frac{\beta}{2}}.\) |
Az \(\displaystyle \alpha\) és \(\displaystyle \beta\) egy háromszög szögei, ezért \(\displaystyle \displaystyle{\frac{\alpha}{2}}\) és \(\displaystyle \displaystyle{\frac{\beta}{2}}\) hegyesszögek, tehát (6) jobb oldalának egyik tényezője sem nulla, vagyis
\(\displaystyle \ctg{\frac{\alpha}{2}}\cdot{\ctg{\frac{\beta}{2}}}=2,\)
és éppen ezt akartuk bizonyítani.
Statistics:
26 students sent a solution. 5 points: Balogh Péter, Braun Zsófia, Dancsák Dénes, Gyuricsek Ákos, Inokai Ádám, Iván Máté Domonkos, Pánovics Máté, Szabó Donát, Viczián Márk, Žigo Boglárka. 4 points: Baksa Anna, Bencze Mátyás, Hajdú Ábel, Locher Péter, Márfai Dóra, Papp Zsófia, Simon Bálint, Török Eszter Júlia, Wodala Gréta Klára. 3 points: 1 student. 2 points: 3 students.
Problems in Mathematics of KöMaL, April 2024
