A C. 1816. feladat (2024. május)

C. 1816. Az \(\displaystyle a=14\), \(\displaystyle b=13\), \(\displaystyle c=15\) hosszúságú oldalakkal rendelkező háromszög oldalai érintik az \(\displaystyle R=5\) sugarú gömböt. Határozzuk meg a gömb középpontja és a háromszög síkja közötti távolságot.

horvát versenyfeladat

(5 pont)

A beküldési határidő 2024. június 10-én LEJÁRT.

Megoldás. A gömb minden síkmetszete kör, ezért a háromszög síkja egy körben metszi a gömb felületét, ez a kör a feltétel alapján a háromszög beírt köre, amelynek \(\displaystyle r\) sugarát a

\(\displaystyle T=r\cdot s\)

összefüggés alapján, a

\(\displaystyle T=\sqrt{s\cdot(s-a)\cdot(s-b)\cdot(s-c)}\)

Héron-képlet alkalmazásával számíthatjuk ki, ahol \(\displaystyle s\) a háromszög félkerülete.

A feltételek alapján \(\displaystyle 2s=a+b+c=42\), ezért \(\displaystyle s=21\), így a háromszög területe

Az (1) eredményből \(\displaystyle T=r\cdot s\) alapján azt kapjuk, hogy

\(\displaystyle r=4.\)

Tekintsük a következő ábrát, amelyen a gömb \(\displaystyle O\) középpontjából a háromszög \(\displaystyle S\) síkjára bocsátott merőleges talppontját \(\displaystyle T\)-vel jelöltük.

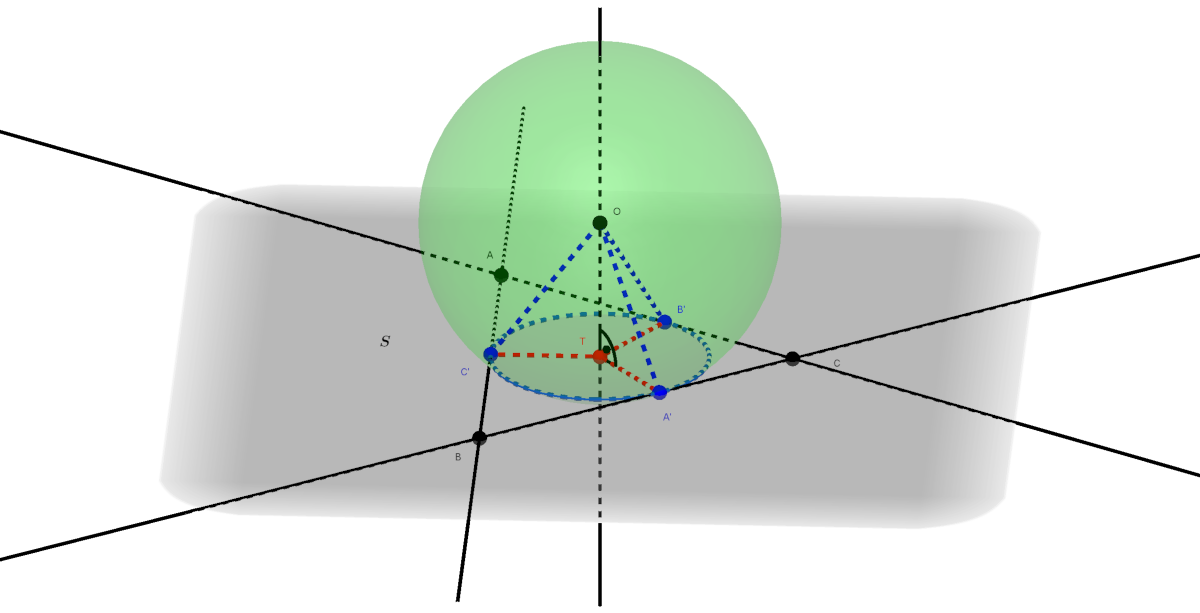
Az ábrán az \(\displaystyle ABC\) háromszög síkja metszi a gömböt, a háromszög \(\displaystyle BC\), \(\displaystyle CA\), \(\displaystyle AB\) oldalai rendre az \(\displaystyle A'\), \(\displaystyle B'\), \(\displaystyle C'\) pontokban érintik a gömböt és így a háromszög \(\displaystyle 4\) egység sugarú beírt körét.

Mivel az \(\displaystyle A'\), \(\displaystyle B'\), \(\displaystyle C'\) pontok rajta vannak a gömb felületén, ezért

\(\displaystyle OA'=OB'=OC'=5.\)

Az \(\displaystyle OT\) egyenes merőleges az \(\displaystyle S\) sík minden egyenesére, így az \(\displaystyle A'T\) egyenesre is, tehát az \(\displaystyle A'OT\) háromszög a \(\displaystyle T\) pontban derékszögű háromszög.

Ebből a Pitagorasz-tétel felhasználásával kapjuk, hogy \(\displaystyle OT=3\), vagyis a gömb középpontjának és a háromszög síkjának távolsága \(\displaystyle 3\).

Statisztika:

46 dolgozat érkezett.
5 pontot kapott:	Baksa Anna, Balogh Péter, Barna Márton, Bencze Mátyás, Biborka Bernadett, Braun Zsófia, Gerencsér László, Gyuricsek Ákos, Inokai Ádám, Iván Máté Domonkos, Juhos Bálint András, Márfai Dóra, Monoczki Máté, Nagy 292 Korina, Pánovics Máté, Papp Zsófia, Simon Bálint, Somogyi Dóra, Szabó Donát, Török Eszter Júlia, Viczián Márk, Zétényi Áron, Žigo Boglárka.
4 pontot kapott:	Antónyi Emő, Demeter Flóra, Fülöp Máté, Hajdú Ábel, Oleár Ákos, Palásthy Bánk, Polyányi Lora Molli, Puskás Péter, Raffay Gergely, Volford Barnabás, Wodala Gréta Klára.
3 pontot kapott:	6 versenyző.
1 pontot kapott:	1 versenyző.
0 pontot kapott:	1 versenyző.

A KöMaL 2024. májusi matematika feladatai