A C. 1819. feladat (2024. szeptember)

C. 1819. Legyen $\displaystyle ABCD$ egységoldalú négyzet, és legyen az $\displaystyle A$ középpontú $\displaystyle AC$ sugarú kör $\displaystyle k$. Legyen $\displaystyle k$-nak az $\displaystyle AB$ félegyenessel $\displaystyle B$-n túl vett metszéspontja $\displaystyle E$, míg az $\displaystyle AD$ félegyenessel $\displaystyle D$-n túl vett metszéspontja $\displaystyle F$. Messe az $\displaystyle EF$ egyenes $\displaystyle BC$-t $\displaystyle G$-ben, és tükrözzük $\displaystyle B$-t $\displaystyle AG$ egyenesre, legyen a tükörkép $\displaystyle H$. Hány egység hosszú a $\displaystyle HE$ szakasz?

Javasolta: Hegedűs Dániel, Gyöngyös

(5 pont)

A beküldési határidő 2024. október 10-én LEJÁRT.

Megoldás. Tekintsük a következő ábrát:

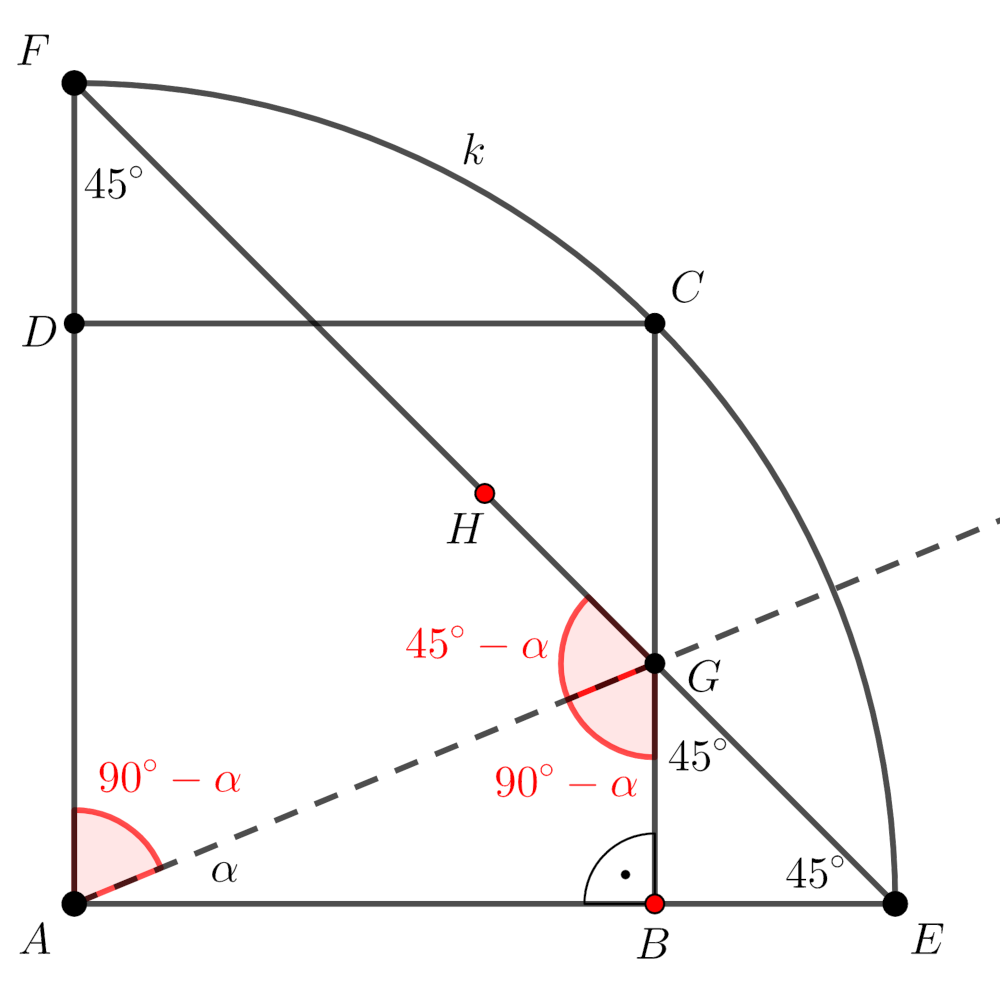
Tudjuk, hogy $\displaystyle ABCD$ egységnyi oldalú négyzet, ezért $\displaystyle AB=BC=CD=DA=1$, tehát $\displaystyle AC=\sqrt{2}$. Az $\displaystyle AEF$ háromszög egyenlő szárú és derékszögű, így $\displaystyle AEF\sphericalangle=AFE\sphericalangle=45^{\circ}$, ezért a $\displaystyle BEG$ derékszögű háromszög egyik hegyesszöge $\displaystyle 45^{\circ}$, ami azt jelenti, hogy a $\displaystyle BEG$ is egyenlő szárú derékszögű háromszög. Az előzőek alapján felírható, hogy

$\displaystyle AF=AC=AE=r = \sqrt{2},$

$\displaystyle EF= \sqrt{2}AE=2,$

$\displaystyle BE=BG = \sqrt{2}-1,$

$\displaystyle EG = \sqrt{2}BG=2-\sqrt{2}.$

Azt már láttuk (1) alapján, hogy az $\displaystyle FAG$ háromszög $\displaystyle AF$ oldala $\displaystyle \sqrt{2}$, ugyanakkor az $\displaystyle FG$ oldalát felírva a (2) és a (4) segítségével azt kapjuk, hogy $\displaystyle \displaystyle{FG=EF-EG=2-(2-\sqrt{2})=\sqrt{2}}$. Ez azt jelenti, hogy az $\displaystyle FAG$ háromszög egyenlő szárú, tehát

$\displaystyle FAG\sphericalangle=AGF\sphericalangle,$

amiből az következik, hogy

$\displaystyle AGF\sphericalangle=AGB\sphericalangle.$

Vagyis a $\displaystyle B$ pont $\displaystyle AG$ egyenesre vonatkozó tükörképe éppen az $\displaystyle FE$ egyenesre esik, vagyis $\displaystyle H\in FE$.
Így tehát

$\displaystyle HE=HG+GE=BG+GE=\sqrt{2}-1+2-\sqrt{2}=1.$

Statisztika:

206 dolgozat érkezett.
5 pontot kapott:	Abonyi Donát Tibor, Balogh Péter, Bencze Mátyás, Benedek Kinyó, Bense Tamás, Budai Máté, Csáki Anikó, Csiszár András, Danka Emma, Farkas András, Gaál Gergely, Gál András, Göőz Lilla, Gyöngyösi Dorottya, Halmosi Dávid, Hetyei Dániel, Hicsó Máté Kristóf, Hollósi Dominik, Iván Máté Domonkos, Kókai Ákos, Kudomrák Lili Anna , Li Mingdao, Lovas Márk, Magura Anna Luca, Major Csilla, Maróti Olga, Masa Barnabás, Mateas Isabelle, Mezei Marcell, Miszori Márton, Molnár Lili, Nagypál Katóca, Nelissen Sámuel Zalán, Oláh András, Ördög Dávid, Palásthy Bánk, Pánovics Máté, Papp Emese Petra, Pázmándi Renáta , Pink István, Radošická Emma, Rózsa Zsombor, Szabó Máté, Szalóki Árpád, Tóth Luca, Török Eszter Júlia, Viczián Adél, Wodala Gréta Klára.
4 pontot kapott:	19 versenyző.
3 pontot kapott:	19 versenyző.
2 pontot kapott:	25 versenyző.
1 pontot kapott:	30 versenyző.
0 pontot kapott:	37 versenyző.
Nem számítjuk a versenybe a születési dátum vagy a szülői nyilatkozat hiánya miatt:	16 dolgozat.

A KöMaL 2024. szeptemberi matematika feladatai