A C. 1822. feladat (2024. szeptember)

C. 1822. Az $\displaystyle ABCD$ konvex négyszög $\displaystyle AC$ és $\displaystyle BD$ átlói az $\displaystyle M$ pontban metszik egymást. Az átlók által létrehozott $\displaystyle ABM$, $\displaystyle BCM$, $\displaystyle CDM$ és $\displaystyle DAM$ háromszögek területének számértékei rendre az $\displaystyle a$, $\displaystyle b$, $\displaystyle c$, $\displaystyle d$ pozitív egész számok.

$\displaystyle a)$ Bizonyítsuk be, hogy $\displaystyle a\cdot b\cdot c\cdot d$ négyzetszám.

$\displaystyle b)$ Tegyük fel, hogy az $\displaystyle a$, $\displaystyle b$, $\displaystyle c$, $\displaystyle d$ számok között pontosan két, egymástól különböző páratlan prímszám van. Határozzuk meg az $\displaystyle a$, $\displaystyle b$, $\displaystyle c$, $\displaystyle d$ számokat úgy, hogy az $\displaystyle ABCD$ négyszög területe a lehető legkisebb négyzetszám legyen.

Javasolta: Bíró Bálint, Eger

(5 pont)

A beküldési határidő 2024. október 10-én LEJÁRT.

Megoldás. $\displaystyle a)$ Tekintsük az alábbi ábrát.

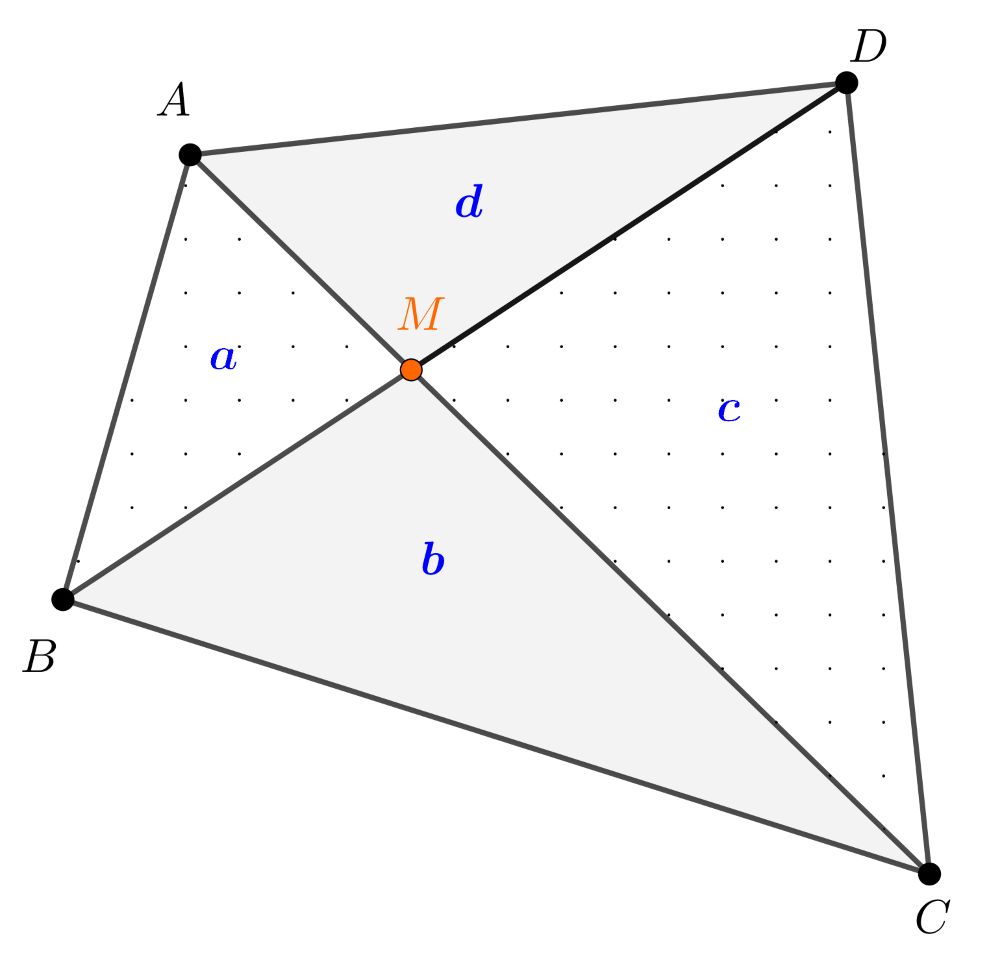
Az $\displaystyle ABM$ és $\displaystyle BCM$ háromszögeknek a $\displaystyle B$ csúcshoz tartozó magassága közös, ezért területeik aránya az $\displaystyle AM$ és $\displaystyle BM$ alapok hosszának arányával egyezik meg, azaz

Hasonlóképpen a $\displaystyle DAM$ és $\displaystyle CDM$ háromszögeknek a $\displaystyle D$ csúcshoz tartozó magassága közös, tehát területeik aránya a megfelelő alapok hosszának arányával egyenlő, vagyis

Az (1) és (2) eredmények szerint

$\displaystyle \displaystyle{\frac{a}{b}=\frac{d}{c}},$

ezért

(3) viszont azt jelenti, hogy $\displaystyle a\cdot{c}\cdot{b}\cdot{d}=(a\cdot{c})^2=(b\cdot{d})^2$, és mivel $\displaystyle a$, $\displaystyle b$, $\displaystyle c$, $\displaystyle d$ pozitív egészek, ezért $\displaystyle a\cdot c\cdot b\cdot d$ valóban négyzetszám.

$\displaystyle b)$ Nem sérti az általánosságot, ha feltesszük, hogy az $\displaystyle a$ prímszám. Ekkor két lehetséges eset van:
1) $\displaystyle b$ és $\displaystyle d$ közül pontosan az egyik prím,
vagy
2) $\displaystyle c$ prímszám.

Tekintsük először az 1) esetet.

Feltehetjük, hogy $\displaystyle d$ prímszám, ekkor a feltételnek megfelelően $\displaystyle b$ és $\displaystyle c$ nem prímek. Az $\displaystyle a)$ feladatrészben igazoltuk, hogy

$\displaystyle a\cdot c=b\cdot d,$

ebből az következik, hogy a $\displaystyle d$ prím osztója a $\displaystyle c$ számnak, hiszen $\displaystyle a$-nak nem lehet osztója, mivel $\displaystyle a$ és $\displaystyle d$ különböző prímek.

Ezért

$\displaystyle c=k\cdot d,$

ahol $\displaystyle k\neq{1}$, hiszen $\displaystyle c$ nem prím.

Ekkor azonban az $\displaystyle a\cdot c=b\cdot d$ összefüggésből azt kapjuk, hogy

$\displaystyle b=k\cdot a.$

Az $\displaystyle ABCD$ négyszög $\displaystyle T$ területére teljesül, hogy

$\displaystyle T=a+b+c+d,$

ebből előző eredményeink alapján $\displaystyle T=a+k\cdot a+k\cdot d+d$ adódik, amelyből szorzattá alakítás után következik, hogy

A $\displaystyle T$ szám négyzetszám kell legyen, mégpedig a feltételek és annak figyelembe vételével, hogy $\displaystyle a+d$ páros, a lehető legkisebb páros négyzetszám.

Kézenfekvő tehát, hogy kis értékű páratlan $\displaystyle a$, $\displaystyle d$ prímeket keressünk.

Az általánosság megsértése nélkül feltehető, hogy $\displaystyle a<d$, ezért ha például $\displaystyle a=3$ és $\displaystyle d=5$, akkor $\displaystyle a+d=8$, így $\displaystyle k+1=2$ esetén azt kapjuk, hogy $\displaystyle T=16$, amely négyzetszám ugyan, de ez mégsem felel meg a feltételeknek, hiszen ekkor $\displaystyle k=1$ lenne. Így $\displaystyle a=3$ és $\displaystyle d=5$ mellett $\displaystyle k+1$ értéke legalább $\displaystyle 8$, azaz $\displaystyle T$ legalább $\displaystyle 64$.

Egyszerű számolással beláthatjuk, hogy ennél kisebb $\displaystyle T$ négyzetszámot csak akkor kaphatunk, ha

$\displaystyle a=5, \quad d=7,$

ekkor $\displaystyle k+1=3$, vagyis $\displaystyle k=2$ mellett

Tekintsük most a 2) lehetőséget, vagyis azt, amikor $\displaystyle a$ mellett $\displaystyle c$ a másik prímszám, itt is feltehetjük, hogy $\displaystyle a<c$.

Ebből egyrészt az következik, hogy $\displaystyle b$ és $\displaystyle d$ egyike sem prím, másrészt $\displaystyle a\cdot c=b\cdot d$ alapján $\displaystyle b\cdot d$ két prím szorzata, amely csak úgy állhat fenn, ha a $\displaystyle b$ és $\displaystyle d$ közül valamelyik szám értéke $\displaystyle 1$.

Legyen például $\displaystyle b=1$, ekkor nyilvánvaló, hogy

Mivel $\displaystyle T$ értékére ismét a lehető legkisebb négyzetszámot keressük, ezért $\displaystyle a=3, c=5$ és $\displaystyle b=1$ mellett (6) szerint $\displaystyle d=15$, ekkor azonban

$\displaystyle T=3+1+5+15=24,$

ez viszont nem négyzetszám. Ha pedig $\displaystyle a=3, c=7$ és $\displaystyle b=1$ mellett $\displaystyle d=21$, akkor

$\displaystyle T=3+1+7+21=32,$

de ez sem négyzetszám.

Könnyen belátható, hogy bármely más $\displaystyle a$, $\displaystyle c$ prímek és $\displaystyle b=1$ esetén a $\displaystyle T$ számra $\displaystyle 36$-nál nagyobb értéket kapunk.

Minden esetet megvizsgáltunk, és azt kaptuk, hogy a feladat feltételeinek az

$\displaystyle a=5, \,d=7,$

illetve $\displaystyle k=2$ miatt

$\displaystyle b=10,\, c=14$

számok felelnek meg, így

$\displaystyle T=36.$

Megjegyzések. 1) Az (5) eredmény $\displaystyle a=5, d=13$ illetve $\displaystyle a=7, d=11$ esetén is elérhető, de mindkét esetben $\displaystyle k=1$, ezért ezekből nem kapunk megoldást.

2) A feltételeknek megfelelő $\displaystyle ABCD$ négyszög valóban létezik. Ha például $\displaystyle AC$ merőleges $\displaystyle BD$-re és $\displaystyle AM=5$, $\displaystyle CM=10$, illetve $\displaystyle BM=2$, valamint $\displaystyle \displaystyle{DM=\frac{14}{5}}$, akkor az $\displaystyle ABM$, $\displaystyle BCM$, $\displaystyle CDM$, $\displaystyle DAM$ háromszögek területe rendre $\displaystyle 5$, $\displaystyle 10$, $\displaystyle 14$, $\displaystyle 7$.

Statisztika:

55 dolgozat érkezett.
5 pontot kapott:	Balog 888 Emese, Balogh Péter, Barna Márton, Budai Máté, Iván Máté Domonkos, Kókai Ákos, Masa Barnabás, Monoczki Máté, Pink István, Wodala Gréta Klára.
4 pontot kapott:	Bencze Mátyás, Márfai Dóra.
3 pontot kapott:	15 versenyző.
2 pontot kapott:	15 versenyző.
1 pontot kapott:	4 versenyző.
0 pontot kapott:	2 versenyző.
Nem számítjuk a versenybe a születési dátum vagy a szülői nyilatkozat hiánya miatt:	2 dolgozat.

A KöMaL 2024. szeptemberi matematika feladatai