 |
A C. 1822. feladat (2024. szeptember) |
C. 1822. Az \(\displaystyle ABCD\) konvex négyszög \(\displaystyle AC\) és \(\displaystyle BD\) átlói az \(\displaystyle M\) pontban metszik egymást. Az átlók által létrehozott \(\displaystyle ABM\), \(\displaystyle BCM\), \(\displaystyle CDM\) és \(\displaystyle DAM\) háromszögek területének számértékei rendre az \(\displaystyle a\), \(\displaystyle b\), \(\displaystyle c\), \(\displaystyle d\) pozitív egész számok.
\(\displaystyle a)\) Bizonyítsuk be, hogy \(\displaystyle a\cdot b\cdot c\cdot d\) négyzetszám.
\(\displaystyle b)\) Tegyük fel, hogy az \(\displaystyle a\), \(\displaystyle b\), \(\displaystyle c\), \(\displaystyle d\) számok között pontosan két, egymástól különböző páratlan prímszám van. Határozzuk meg az \(\displaystyle a\), \(\displaystyle b\), \(\displaystyle c\), \(\displaystyle d\) számokat úgy, hogy az \(\displaystyle ABCD\) négyszög területe a lehető legkisebb négyzetszám legyen.
Javasolta: Bíró Bálint, Eger
(5 pont)
A beküldési határidő 2024. október 10-én LEJÁRT.
Megoldás. \(\displaystyle a)\) Tekintsük az alábbi ábrát.
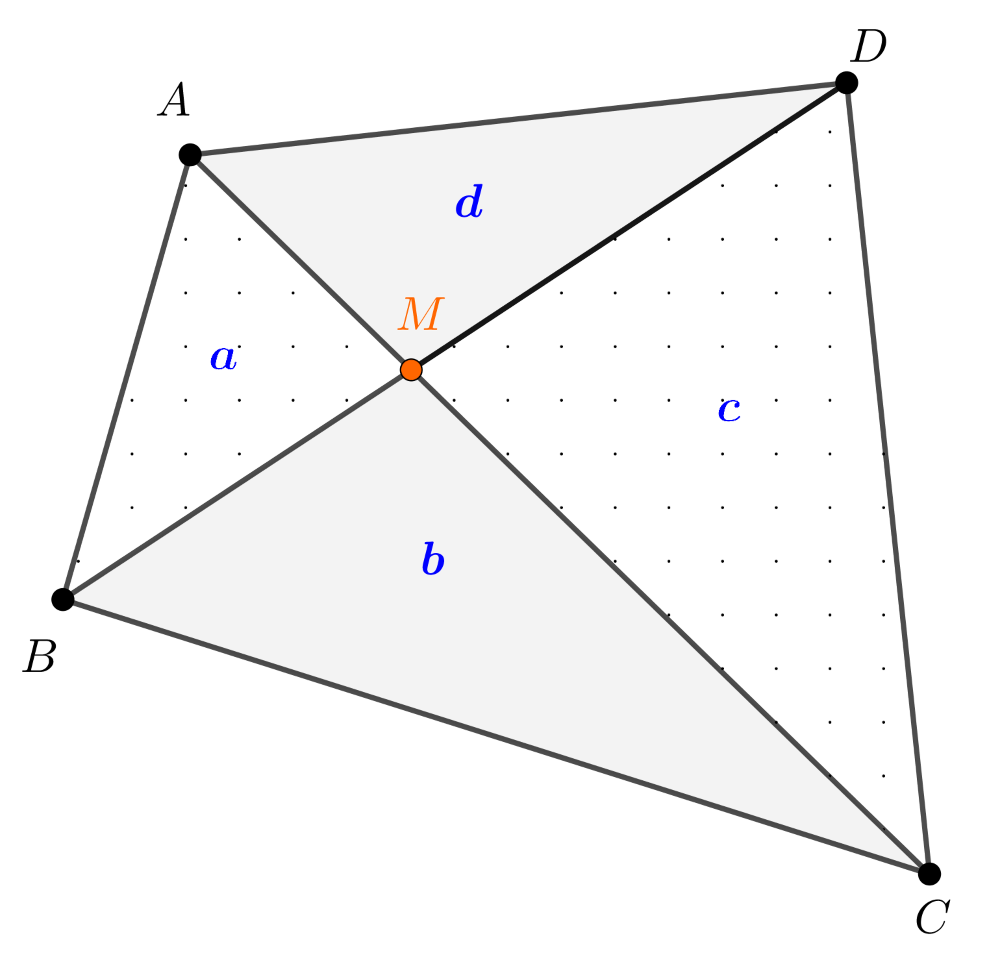
Az \(\displaystyle ABM\) és \(\displaystyle BCM\) háromszögeknek a \(\displaystyle B\) csúcshoz tartozó magassága közös, ezért területeik aránya az \(\displaystyle AM\) és \(\displaystyle BM\) alapok hosszának arányával egyezik meg, azaz
| \(\displaystyle (1)\) | \(\displaystyle \displaystyle{\frac{a}{b}=\frac{AM}{MC}}.\) |
Hasonlóképpen a \(\displaystyle DAM\) és \(\displaystyle CDM\) háromszögeknek a \(\displaystyle D\) csúcshoz tartozó magassága közös, tehát területeik aránya a megfelelő alapok hosszának arányával egyenlő, vagyis
| \(\displaystyle (2)\) | \(\displaystyle \displaystyle{\frac{d}{c}=\frac{AM}{MC}}.\) |
Az (1) és (2) eredmények szerint
\(\displaystyle \displaystyle{\frac{a}{b}=\frac{d}{c}},\)
ezért
| \(\displaystyle (3)\) | \(\displaystyle a\cdot c=b\cdot d. \) |
(3) viszont azt jelenti, hogy \(\displaystyle a\cdot{c}\cdot{b}\cdot{d}=(a\cdot{c})^2=(b\cdot{d})^2\), és mivel \(\displaystyle a\), \(\displaystyle b\), \(\displaystyle c\), \(\displaystyle d\) pozitív egészek, ezért \(\displaystyle a\cdot c\cdot b\cdot d\) valóban négyzetszám.
\(\displaystyle b)\) Nem sérti az általánosságot, ha feltesszük, hogy az \(\displaystyle a\) prímszám. Ekkor két lehetséges eset van:
1) \(\displaystyle b\) és \(\displaystyle d\) közül pontosan az egyik prím,
vagy
2) \(\displaystyle c\) prímszám.
Tekintsük először az 1) esetet.
Feltehetjük, hogy \(\displaystyle d\) prímszám, ekkor a feltételnek megfelelően \(\displaystyle b\) és \(\displaystyle c\) nem prímek. Az \(\displaystyle a)\) feladatrészben igazoltuk, hogy
\(\displaystyle a\cdot c=b\cdot d,\)
ebből az következik, hogy a \(\displaystyle d\) prím osztója a \(\displaystyle c\) számnak, hiszen \(\displaystyle a\)-nak nem lehet osztója, mivel \(\displaystyle a\) és \(\displaystyle d\) különböző prímek.
Ezért
\(\displaystyle c=k\cdot d, \)
ahol \(\displaystyle k\neq{1}\), hiszen \(\displaystyle c\) nem prím.
Ekkor azonban az \(\displaystyle a\cdot c=b\cdot d\) összefüggésből azt kapjuk, hogy
\(\displaystyle b=k\cdot a.\)
Az \(\displaystyle ABCD\) négyszög \(\displaystyle T\) területére teljesül, hogy
\(\displaystyle T=a+b+c+d,\)
ebből előző eredményeink alapján \(\displaystyle T=a+k\cdot a+k\cdot d+d\) adódik, amelyből szorzattá alakítás után következik, hogy
| \(\displaystyle (4)\) | \(\displaystyle T=(a+d)\cdot(k+1).\) |
A \(\displaystyle T\) szám négyzetszám kell legyen, mégpedig a feltételek és annak figyelembe vételével, hogy \(\displaystyle a+d\) páros, a lehető legkisebb páros négyzetszám.
Kézenfekvő tehát, hogy kis értékű páratlan \(\displaystyle a\), \(\displaystyle d\) prímeket keressünk.
Az általánosság megsértése nélkül feltehető, hogy \(\displaystyle a<d\), ezért ha például \(\displaystyle a=3\) és \(\displaystyle d=5\), akkor \(\displaystyle a+d=8\), így \(\displaystyle k+1=2\) esetén azt kapjuk, hogy \(\displaystyle T=16\), amely négyzetszám ugyan, de ez mégsem felel meg a feltételeknek, hiszen ekkor \(\displaystyle k=1\) lenne. Így \(\displaystyle a=3\) és \(\displaystyle d=5\) mellett \(\displaystyle k+1\) értéke legalább \(\displaystyle 8\), azaz \(\displaystyle T\) legalább \(\displaystyle 64\).
Egyszerű számolással beláthatjuk, hogy ennél kisebb \(\displaystyle T\) négyzetszámot csak akkor kaphatunk, ha
\(\displaystyle a=5, \quad d=7,\)
ekkor \(\displaystyle k+1=3\), vagyis \(\displaystyle k=2\) mellett
| \(\displaystyle (5)\) | \(\displaystyle T=36.\) |
Tekintsük most a 2) lehetőséget, vagyis azt, amikor \(\displaystyle a\) mellett \(\displaystyle c\) a másik prímszám, itt is feltehetjük, hogy \(\displaystyle a<c\).
Ebből egyrészt az következik, hogy \(\displaystyle b\) és \(\displaystyle d\) egyike sem prím, másrészt \(\displaystyle a\cdot c=b\cdot d\) alapján \(\displaystyle b\cdot d\) két prím szorzata, amely csak úgy állhat fenn, ha a \(\displaystyle b\) és \(\displaystyle d\) közül valamelyik szám értéke \(\displaystyle 1\).
Legyen például \(\displaystyle b=1\), ekkor nyilvánvaló, hogy
| \(\displaystyle (6)\) | \(\displaystyle d=a\cdot c.\) |
Mivel \(\displaystyle T\) értékére ismét a lehető legkisebb négyzetszámot keressük, ezért \(\displaystyle a=3, c=5\) és \(\displaystyle b=1\) mellett (6) szerint \(\displaystyle d=15\), ekkor azonban
\(\displaystyle T=3+1+5+15=24,\)
ez viszont nem négyzetszám. Ha pedig \(\displaystyle a=3, c=7\) és \(\displaystyle b=1\) mellett \(\displaystyle d=21\), akkor
\(\displaystyle T=3+1+7+21=32,\)
de ez sem négyzetszám.
Könnyen belátható, hogy bármely más \(\displaystyle a\), \(\displaystyle c\) prímek és \(\displaystyle b=1\) esetén a \(\displaystyle T\) számra \(\displaystyle 36\)-nál nagyobb értéket kapunk.
Minden esetet megvizsgáltunk, és azt kaptuk, hogy a feladat feltételeinek az
\(\displaystyle a=5, \,d=7,\)
illetve \(\displaystyle k=2\) miatt
\(\displaystyle b=10,\, c=14\)
számok felelnek meg, így
\(\displaystyle T=36.\)
Megjegyzések. 1) Az (5) eredmény \(\displaystyle a=5, d=13\) illetve \(\displaystyle a=7, d=11\) esetén is elérhető, de mindkét esetben \(\displaystyle k=1\), ezért ezekből nem kapunk megoldást.
2) A feltételeknek megfelelő \(\displaystyle ABCD\) négyszög valóban létezik. Ha például \(\displaystyle AC\) merőleges \(\displaystyle BD\)-re és \(\displaystyle AM=5\), \(\displaystyle CM=10\), illetve \(\displaystyle BM=2\), valamint \(\displaystyle \displaystyle{DM=\frac{14}{5}}\), akkor az \(\displaystyle ABM\), \(\displaystyle BCM\), \(\displaystyle CDM\), \(\displaystyle DAM\) háromszögek területe rendre \(\displaystyle 5\), \(\displaystyle 10\), \(\displaystyle 14\), \(\displaystyle 7\).
Statisztika:
55 dolgozat érkezett. 5 pontot kapott: Balog 888 Emese, Balogh Péter, Barna Márton, Budai Máté, Iván Máté Domonkos, Kókai Ákos, Masa Barnabás, Monoczki Máté, Pink István, Wodala Gréta Klára. 4 pontot kapott: Bencze Mátyás, Márfai Dóra. 3 pontot kapott: 15 versenyző. 2 pontot kapott: 15 versenyző. 1 pontot kapott: 4 versenyző. 0 pontot kapott: 2 versenyző. Nem számítjuk a versenybe a születési dátum vagy a szülői nyilatkozat hiánya miatt: 2 dolgozat.
A KöMaL 2024. szeptemberi matematika feladatai