 |
A C. 1825. feladat (2024. október) |
C. 1825. Az e egyenes a k1 kört a különböző A és B pontokban metszi. A k2 kör a C pontban érinti a k1 kört és a D pontban az e egyenest. A CD egyenes és a k1 kör másik metszéspontja T. Mutassuk meg, hogy AT=TB.
Svájci olimpiai feladat
(5 pont)
A beküldési határidő 2024. november 11-én LEJÁRT.
Megoldás. Jelöljük a k1, illetve k2 kör középpontját O-val, illetve K-val, a CD egyenest f-fel és legyen KDC∢=α.
Tekintsük az alábbi ábrát.
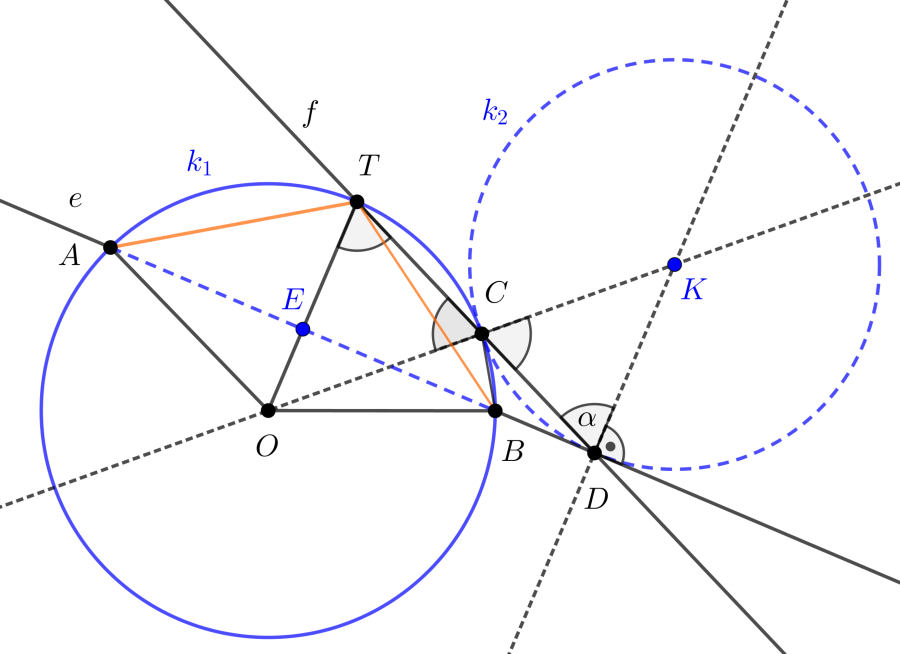
Az e egyenes a k2 kör érintője, ezért KD⊥e.
A KDC háromszög egyenlő szárú, mert KC=KD a k2 kör sugarai, ebből KCD∢=α következik. Ugyanakkor KCD∢ és TCO∢ csúcsszögek, ezért egyenlők, így
TCO∢=α.
A k1 körben OC=OT sugarak, így az OTC háromszög egyenlő szárú, ezért
| (1) | CTO∢=α. |
Az (1) összefüggés szerint KDC∢=CTO∢, így az OT és KD az f egyenessel ugyanakkora szöget zár be, vagyis OT és KD párhuzamos egyenesek.
Ebből azonnal adódik, hogy OT⊥e, tehát OT a k1 kör AB húrját merőlegesen felezi az E pontban, másrészt felezi a k1 kör T pontot is tartalmazó AB ívét éspedig éppen a T pontban.
Az egyenlő hosszúságú ívekhez egyenlő hosszú húrok tartoznak, eszerint valóban teljesül, hogy AT=TB.
Megjegyzések. 1) A feltételek miatt a k2 kör sem az A, sem a B pontban nem érintheti az e egyenest.
2) Bizonyítható, hogy a C pont helyzetének változtatásával a T pontnak kétféle helyzete jöhet létre a k1 körön, ezek az e egyenesre vonatkozóan egymás tükörképei.
Statisztika:
141 dolgozat érkezett. 5 pontot kapott: Aaishipragya Kahaly, Albert Luca Liliána, Balogh Péter, Békési Máté, Bense Tamás, Blaskovics Bálint, Bodó Rókus Dániel, Bubálik Nóra, Budai Máté, Farkas András, Fejes-Tóth Fanni, Fülöp Magdaléna, Hajnal Ákos Huba, Halász Tamás, Hetyei Dániel, Hollósi Dominik, Iván Máté Domonkos, Kókai Ákos, Li Tanran, Lovas Márk, Maróti Olga, Mateas Isabelle, Medgyesi Júlia, Menyhárt Eszter Panna, Mezei Marcell, Molnár-Sáska Tamás, Nagypál Katóca, Papp Emese Petra, Pázmándi Renáta , Pink István, Szalóki Árpád, Válek Péter. 4 pontot kapott: 24 versenyző. 3 pontot kapott: 11 versenyző. 2 pontot kapott: 7 versenyző. 1 pontot kapott: 6 versenyző. 0 pontot kapott: 37 versenyző. Nem számítjuk a versenybe a születési dátum vagy a szülői nyilatkozat hiánya miatt: 13 dolgozat.
A KöMaL 2024. októberi matematika feladatai
|
|

