A C. 1829. feladat (2024. november)

C. 1829. Az egységnyi oldalú $\displaystyle ABCD$ négyzet $\displaystyle AB$ oldalán úgy vettük fel az $\displaystyle E$, $\displaystyle BC$ oldalán pedig az $\displaystyle F$ pontot, hogy $\displaystyle EDF\sphericalangle=45^{\circ}$. Határozzuk meg az $\displaystyle EBF$ háromszög kerületének pontos értékét.

Javasolta: Bíró Bálint (Eger)

(5 pont)

A beküldési határidő 2024. december 10-én LEJÁRT.

1. megoldás. Az $\displaystyle E$, $\displaystyle F$ pontok a megfelelő oldalak belső pontjai, mert ha $\displaystyle E$ és $\displaystyle A$ egybeesne, akkor az $\displaystyle EDF\sphericalangle=45^{\circ}$ feltétel miatt $\displaystyle F=B$, ha pedig $\displaystyle E$ és $\displaystyle B$ lenne azonos, akkor $\displaystyle F=C$ valósulna meg, de az $\displaystyle EBF$ háromszög egyik esetben sem jönne létre.

Tekintsük az 1. ábrát, amelyen az $\displaystyle EB=x$, $\displaystyle FB=y$, $\displaystyle EF=z$, valamint $\displaystyle ADE\sphericalangle=\alpha$, $\displaystyle CDF\sphericalangle=\beta$ jelöléseket alkalmaztuk.

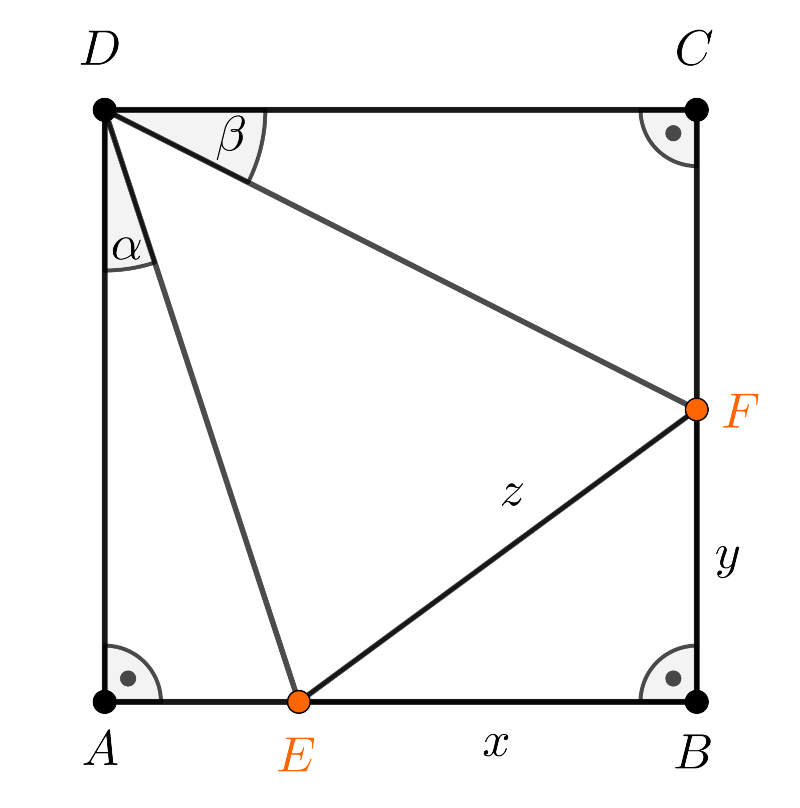
1. ábra

A választott jelölésekkel egyrészt $\displaystyle EA=1-x$, $\displaystyle FC=1-y$, másrészt $\displaystyle \alpha+\beta=45^{\circ}$.

Jelöljük $\displaystyle F'$-vel a $\displaystyle BA$ félegyenesnek az $\displaystyle A$-n túl elhelyezkedő pontját úgy, hogy $\displaystyle AF'=1-y$ teljesüljön (2. ábra).

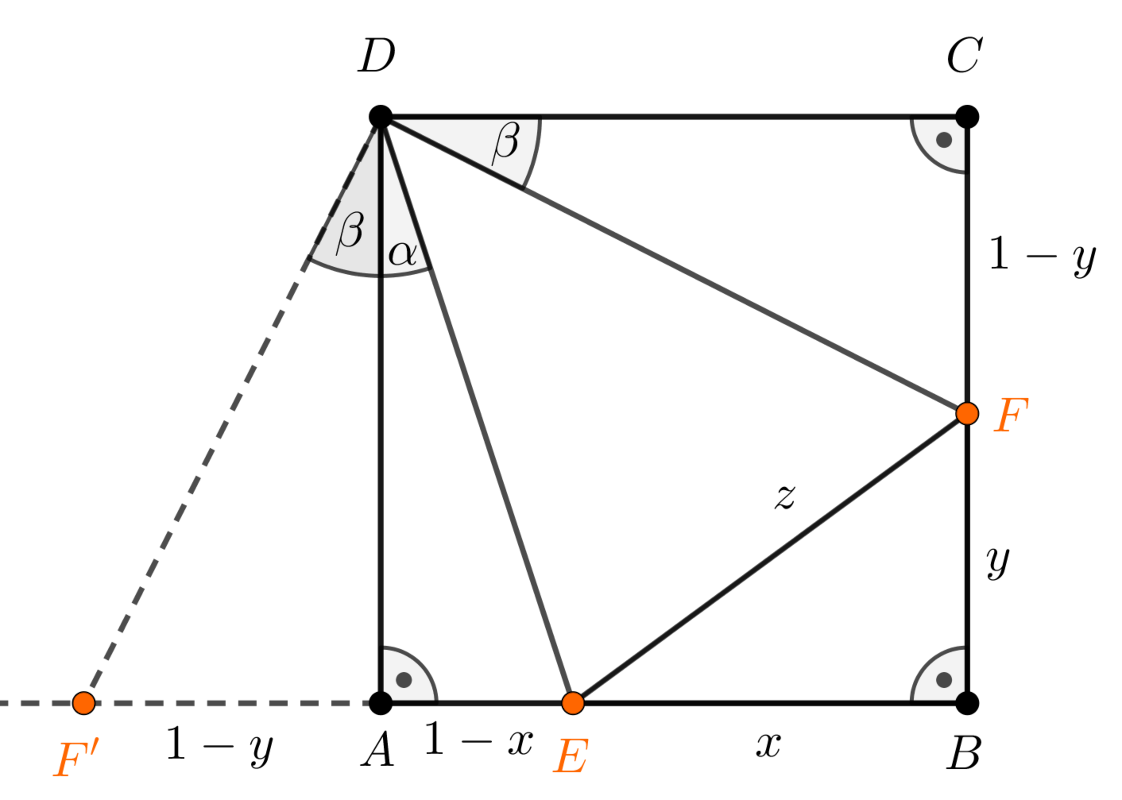
2. ábra

Világos, hogy $\displaystyle FDC$ és $\displaystyle F'DA$ egybevágó derékszögű háromszögek, ezért $\displaystyle F'DA\sphericalangle=\beta$, illetve $\displaystyle F'D=FD$.

Az $\displaystyle \alpha+\beta=45^{\circ}$ feltétel miatt $\displaystyle F'DE\sphericalangle=45^{\circ}$.

Az $\displaystyle F'DE$ és $\displaystyle FDE$ háromszögekben $\displaystyle ED$ közös, $\displaystyle F'D=FD$ és a két háromszögben a két-két oldal által bezárt szög $\displaystyle 45^{\circ}$-os, tehát a két háromszög egybevágó.

Ez pontosan azt jelenti, hogy a $\displaystyle D$ csúccsal szemben levő oldalak is egyenlők, azaz $\displaystyle F'E=FE$, amelyből $\displaystyle 1-x+1-y=z$ következik, innen pedig $\displaystyle x+y+z=2$, tehát az $\displaystyle EBF$ háromszög kerülete

$\displaystyle K_{EBF}=x+y+z=2.$

2. megoldás. Használjuk az 1. ábra jelöléseit, ezekkel

Alkalmazzuk a $\displaystyle \displaystyle{\tg(\alpha+\beta)=\frac{\tg\alpha+\tg\beta}{1-\tg\alpha\cdot\tg\beta}}$ trigonometrikus azonosságot.

Mivel $\displaystyle \alpha+\beta=45^{\circ}$, ezért $\displaystyle \tg(\alpha+\beta)=1$, így (1) alapján

$\displaystyle \displaystyle{1=\frac{1-x+1-y}{1-(1-x)\cdot(1-y)}},$

ahonnan a műveletek elvégzésével és rendezéssel kapjuk, hogy

A (2) összefüggésből következik, hogy $\displaystyle \displaystyle{x^2+y^2+2xy=\frac{4+x^2y^2+4xy}{4}}$, innen pedig $\displaystyle 4$-gyel való szorzással és rendezéssel

Az $\displaystyle EBF$ háromszögre felírt Pitagorasz-tétel szerint $\displaystyle x^2+y^2=z^2$, ebből (3) felhasználásával kapjuk, hogy

Mivel $\displaystyle x<1$ és $\displaystyle y<1$, ezért $\displaystyle 2-xy>0$, tehát (4)-ből

$\displaystyle 2z=2-xy$

adódik, (2)-ből pedig

$\displaystyle 2x+2y=2+xy.$

Az utoljára kapott két egyenlet megfelelő oldalait összeadva $\displaystyle 2x+2y+2z=4$, ezért az $\displaystyle EBF$ háromszög kerülete

$\displaystyle K_{EBF}=x+y+z=2.$

Megjegyzések. 1) Az 1. megoldásban az $\displaystyle F'DA$ háromszög az $\displaystyle FDC$ háromszög $\displaystyle D$ pont körüli $\displaystyle -90^{\circ}$-os elforgatottja.

2) Egyszerűen belátható, hogy ha $\displaystyle E$ azonos $\displaystyle A$-val vagy $\displaystyle B$-vel, akkor az így létrejövő $\displaystyle EBF$ torz háromszög kerülete ugyancsak $\displaystyle 2$ egység.

3) A feladatban szereplő $\displaystyle EBF$ háromszöget meg is szerkeszthetjük, például az alábbi módon.

Legyen az $\displaystyle AB$ szakasz tetszőleges belső pontja $\displaystyle E$. Rajzoljunk az $\displaystyle E$ pontból érintőt a $\displaystyle D$ középpontú, $\displaystyle DA$ sugarú $\displaystyle k$ negyedkörhöz az alábbi ábra szerint, az érintési pontot $\displaystyle P$-vel jelöljük.

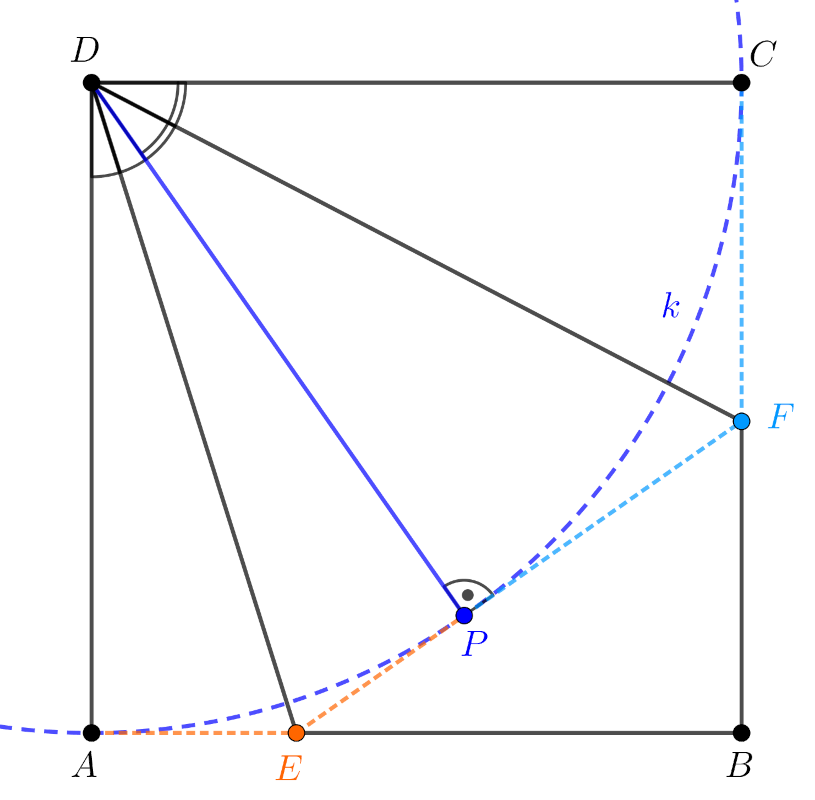
3. ábra

Nyilvánvaló, hogy az $\displaystyle EP$ érintő a $\displaystyle BC$ szakaszt egy belső $\displaystyle F$ pontban metszi. A körhöz külső pontból húzott érintőszakaszok hossza egyenlő, ezért

Tudjuk, hogy $\displaystyle DA=DP=DC=1$, ezért az (5) egyenlőségekből az következik, hogy a $\displaystyle DEA$ és $\displaystyle DEP$ háromszögek egybevágók, hasonlóképpen egybevágók a a $\displaystyle DFP$, illetve $\displaystyle DFC$ háromszögek is. A háromszögek egybevágósága miatt

A (6) és (7) összefüggésekben szereplő szögek összege derékszög, ezért

Az így szerkesztett $\displaystyle E$ és $\displaystyle F$ pontokra tehát teljesül, hogy $\displaystyle EDF\sphericalangle=45^{\circ}$, illetve az 1. és 2. megoldás eredményének megfelelően $\displaystyle K_{EBF}=2$.

Statisztika:

143 dolgozat érkezett.
5 pontot kapott:	60 versenyző.
4 pontot kapott:	3 versenyző.
3 pontot kapott:	8 versenyző.
2 pontot kapott:	20 versenyző.
1 pontot kapott:	9 versenyző.
0 pontot kapott:	24 versenyző.
Nem számítjuk a versenybe a születési dátum vagy a szülői nyilatkozat hiánya miatt:	9 dolgozat.

A KöMaL 2024. novemberi matematika feladatai