A C. 1834. feladat (2024. december)

C. 1834. Három deli herceg versengett Kék király csodálatos leányának kezéért: Piros herceg, Fehér herceg és Zöld herceg. Az első próba a jóízlés próbája volt. A hercegek kaptak egy-egy kék szabályos 20-szöget, amelynek tetszőleges részét átszínezhették a saját színükre, minél ízlésesebben. Azt nem árulta el nekik a királylány, hogy előre eldöntötte, aki a $\displaystyle 20$-szöge ötödénél többet fest át a saját színére, az szerinte túl egoista, és ezért nem folytathatja a vetélkedést a kezéért. Az egyes hercegek az alábbi színezéseket készítették:

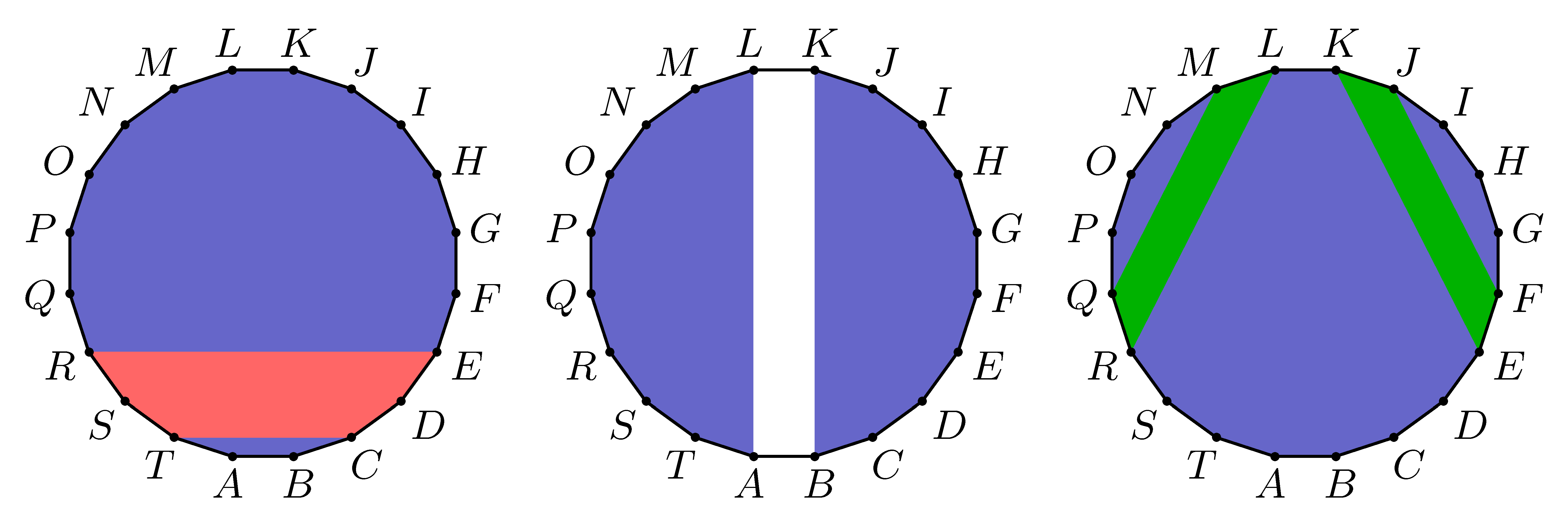
Melyikük jutott tovább a próbák következő fordulójába? (Ahol a feladat egyébként egy hétfejű sárkány legyőzése és megevése volt, de hát az már egy másik matekpélda.)

Javasolta: Bertalan Zoltán (Békéscsaba)

(5 pont)

A beküldési határidő 2025. január 10-én LEJÁRT.

Megoldás. Használjuk a feladat ábráit, a hercegek által kijelölt síkidomok területét jelölje rendre $\displaystyle T_{\text{piros}}$, $\displaystyle T_{\text{fehér}}$ és $\displaystyle T_{\text{zöld}}$, a szabályos húszszögét pedig $\displaystyle T$, továbbá a szabályos sokszög köré írható kör középpontját $\displaystyle X$. A húszszög egy oldalához tartozó egyenlő szárú háromszög szárai legyenek $\displaystyle r$ hosszúságúak, az általuk bezárt szög pedig $\displaystyle 18^{\circ}$, így egy ilyen kis háromszög területe

$\displaystyle \displaystyle{\frac{r^2\cdot \sin{18^{\circ}}}{2}},$

a húszszög területe pedig:

$\displaystyle T=20\cdot \frac{r^2\cdot \sin{18^{\circ}}}{2}=10\cdot r^2\cdot \sin{18^{\circ}}.$

A piros terület a következőképp számolható:

$\displaystyle T_{\text{piros}}=T_{XRST}+T_{XTC}+T_{XCDE}-T_{XRE}=4\cdot \frac{r^2\cdot \sin{18^{\circ}}}{2}+\frac{r^2\cdot \sin{(3\cdot 18^{\circ})}}{2}-\frac{r^2\cdot \sin{(7\cdot 18^{\circ})}}{2}.$

Az utolsó két tag egyenlő, hiszen $\displaystyle (7\cdot 18^{\circ})=180^{\circ}-(3\cdot 18^{\circ})$, ezért $\displaystyle \sin{(3\cdot 18^{\circ}})=\sin{(7\cdot 18^{\circ})}$, tehát

$\displaystyle T_{\text{piros}}=2\cdot r^2\cdot \sin{18^{\circ}}=\frac{T}{5}.$

A fehér területet, vagyis $\displaystyle T_{\text{fehér}}$-et két-két háromszögből fogjuk összerakni:

$\displaystyle T_{\text{fehér}}=T_{ABKL}=T_{XAB}+T_{XBK}+T_{XKL}+T_{XLA}=2\cdot \frac{r^2\cdot \sin{18^{\circ}}}{2}+2\cdot \frac{r^2\cdot \sin{(9\cdot18^{\circ})}}{2}.$

De a fenti megfontolás alapján az utolsó két tag itt is egyenlő, hiszen $\displaystyle \sin{18^{\circ}}=\sin{(9\cdot18^{\circ})}$. Emiatt:

$\displaystyle T_{\text{fehér}}=2\cdot r^2\cdot \sin{18^{\circ}}=\frac{T}{5}.$

A $\displaystyle T_{\text{zöld}}$-et szintén két részből rakhatjuk össze:

$\displaystyle T_{\text{zöld}}=2\cdot T_{LMQR}=2\cdot \big(T_{XLM}+T_{XMQ}+T_{XQR}-T_{XLR}\big)=2\cdot \Bigg(2\cdot \frac{r^2\cdot \sin{18^{\circ}}}{2}+\frac{r^2\cdot \sin{(4\cdot18^{\circ})}}{2}-\frac{r^2\cdot \sin{(6\cdot 18^{\circ})}}{2} \Bigg).$

A nagy zárójelben levő tagok közül az utolsó kettő ismét egyenlő, ezért:

$\displaystyle T_{\text{zöld}}=2\cdot r^2\cdot \sin{18^{\circ}}=\frac{T}{5}.$

Mivel mindegyik herceg azonos területű részét színezte ki a húszszögnek, ezért mindhárman továbbjutottak, vagyis boldogan készülhetnek a próbák következő fordulójára.

Statisztika:

129 dolgozat érkezett.
5 pontot kapott:	57 versenyző.
4 pontot kapott:	8 versenyző.
3 pontot kapott:	8 versenyző.
2 pontot kapott:	17 versenyző.
1 pontot kapott:	3 versenyző.
0 pontot kapott:	16 versenyző.
Nem számítjuk a versenybe a születési dátum vagy a szülői nyilatkozat hiánya miatt:	11 dolgozat.

A KöMaL 2024. decemberi matematika feladatai