 |
A C. 1836. feladat (2024. december) |
C. 1836. Az egyenlő szárú \(\displaystyle ABC\) háromszög \(\displaystyle AB\) alapjának végpontjain áthaladó \(\displaystyle k\) kör az \(\displaystyle AC\), illetve \(\displaystyle BC\) oldalegyeneseket az \(\displaystyle A\), illetve \(\displaystyle B\) pontokban érinti. A \(\displaystyle k\) körnek egy, az \(\displaystyle A\) és \(\displaystyle B\) pontoktól különböző pontja \(\displaystyle P\). Igazoljuk, hogy a \(\displaystyle P\) pontnak az \(\displaystyle AB\) egyenestől mért távolsága legfeljebb akkora, mint az \(\displaystyle AC\) és \(\displaystyle BC\) egyenesektől mért távolságok számtani közepe.
Javasolta: Bíró Bálint (Eger)
(5 pont)
A beküldési határidő 2025. január 10-én LEJÁRT.
Megoldás. Jelöljük a \(\displaystyle k\) kör középpontját \(\displaystyle O\)-val. Mivel \(\displaystyle AC\) és \(\displaystyle BC\) a \(\displaystyle k\) kör érintői, ezért \(\displaystyle OA\) merőleges \(\displaystyle AC\)-re és \(\displaystyle OB\) merőleges \(\displaystyle BC\)-re. Az \(\displaystyle AB\) egyenese az \(\displaystyle ABC\) háromszög síkját két félsíkra, a \(\displaystyle k\) körvonalat két körívre bontja, a két körív egyike a \(\displaystyle C\) ponttal azonos, a másik körív azzal ellentétes félsíkban van.
Válasszuk a \(\displaystyle P\) pontot az utóbbi köríven, a \(\displaystyle P\)-ből az \(\displaystyle AC\), \(\displaystyle BC\), \(\displaystyle AB\) egyenesekre bocsájtott merőlegesek talppontjai rendre \(\displaystyle X\), \(\displaystyle Y\), \(\displaystyle Z\).
A \(\displaystyle P\) pontból az \(\displaystyle A\), \(\displaystyle B\), \(\displaystyle X\), \(\displaystyle Y\), \(\displaystyle Z\) pontokba húzott szakaszok hosszát a megfelelő kisbetűvel jelöljük, alkalmazzuk továbbá a \(\displaystyle CAB\sphericalangle=CBA\sphericalangle=\alpha\) és az \(\displaystyle PBA\sphericalangle=\beta\) jelölést.
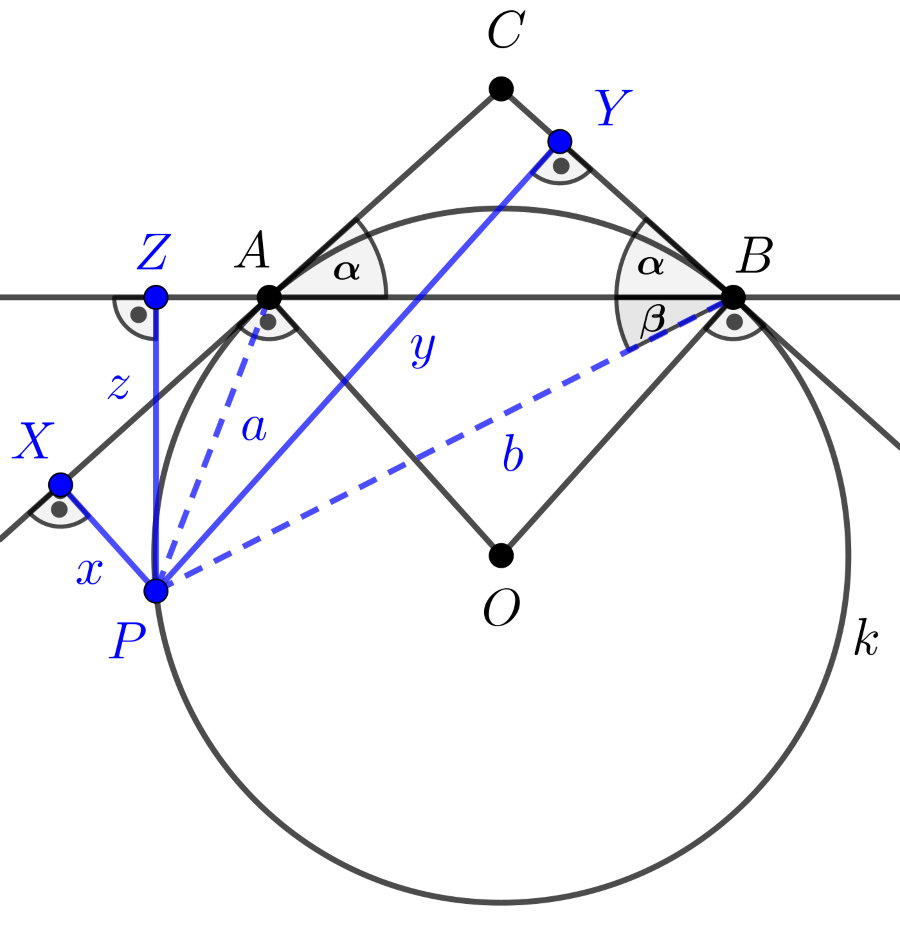
Az ábrán szereplő \(\displaystyle x\), \(\displaystyle y\), \(\displaystyle z\) szakaszokra azt kell bizonyítani, hogy
| \(\displaystyle (1)\) | \(\displaystyle \displaystyle{z\leq\frac{x+y}{2}}.\) |
A kerületi szögek tétele szerint \(\displaystyle PAX\sphericalangle=PBA\sphericalangle=\beta\), hiszen \(\displaystyle PAX\sphericalangle\) a \(\displaystyle k\) körben a \(\displaystyle B\) pontot nem tartalmazó \(\displaystyle AP\) ívhez tartozó érintő szárú kerületi szög, \(\displaystyle PBA\sphericalangle=\beta\) pedig ugyanehhez az ívhez tartozó kerületi szög.
Ebből az következik, hogy a \(\displaystyle PAX\) és \(\displaystyle PBZ\) derékszögű háromszögek hasonlók, és így a megfelelő oldalak aránya egyenlő, vagyis
\(\displaystyle \displaystyle{\frac{a}{x}=\frac{b}{z}},\)
ahonnan azt kapjuk, hogy
| \(\displaystyle (2)\) | \(\displaystyle \displaystyle{\frac{a}{b}=\frac{x}{z}}.\) |
A csúcsszögek egyenlősége miatt \(\displaystyle XAZ\sphericalangle=\alpha\), így \(\displaystyle PAZ\sphericalangle=\alpha+\beta\), továbbá \(\displaystyle PBY\sphericalangle=\alpha+\beta\), ezért a \(\displaystyle PAZ\) és \(\displaystyle PBY\) derékszögű háromszögek szintén hasonlók. Ebből következik, hogy
\(\displaystyle \displaystyle{\frac{a}{z}=\frac{b}{y}},\)
amelyből
| \(\displaystyle (3)\) | \(\displaystyle \displaystyle{\frac{a}{b}=\frac{z}{y}}.\) |
Az (2) és (3) összefüggések együttes figyelembevételével adódik, hogy
\(\displaystyle \displaystyle{\frac{x}{z}=\frac{z}{y}},\)
ahonnan rendezés után
\(\displaystyle z^2=xy,\)
tehát a \(\displaystyle PZ=z\) szakasz hossza a \(\displaystyle PX=x\) és \(\displaystyle PY=y\) szakaszok hosszának mértani közepe.
A számtani és mértani közép közötti egyenlőtlenséget alkalmazva kapjuk, hogy
\(\displaystyle \displaystyle{z\leq\frac{x+y}{2}},\)
ez pedig éppen a bizonyítandó (1) egyenlőtlenség.
Egyenlőség nyilván akkor van, ha \(\displaystyle x=y\), ez pontosan akkor következik be, ha \(\displaystyle PA=PB\), azaz, ha \(\displaystyle P\) felezőpontja a \(\displaystyle k\) kör azon ívének, amelyre illeszkedik.
Ezzel a megoldást befejeztük.
Megjegyzés. A feladat állításának igazolása ugyanígy írható le, ha \(\displaystyle P\) a \(\displaystyle k\) körnek azon ívére illeszkedik, amelyik a \(\displaystyle C\) ponttal azonos félsíkban van, továbbá akkor is, ha a \(\displaystyle Z\) pont az \(\displaystyle AB\) szakasz belső- vagy határpontja. Ha például \(\displaystyle A=Z\), akkor könnyen igazolható, hogy \(\displaystyle B=Y\), így a \(\displaystyle PAX\) és \(\displaystyle PBZ\) derékszögű háromszögek hasonlóságából \(\displaystyle z^2=xy\) azonnal adódik.
Statisztika:
A C. 1836. feladat értékelése még nem fejeződött be.
A KöMaL 2024. decemberi matematika feladatai