 |
A C. 1844. feladat (2025. február) |
C. 1844. Ági pirossal, Laci kékkel színezgeti egy \(\displaystyle n \times n\)-es (\(\displaystyle n>1\)) fehér táblázat mezőit, amely \(\displaystyle i\)-edik sorának \(\displaystyle j\)-edik mezőjét \(\displaystyle (i;j)\)-vel jelöljük. Első lépésben Ági pirosra festi a főátló (bal felsőtől a jobb alsóig) mezőit. Ezután felváltva jönnek: ha Laci \(\displaystyle (i;j)\)-t színezi, akkor Ági \(\displaystyle (j;i)\)-t. Minden mezőt pontosan egyszer színeznek be. A \(\displaystyle k\)-adik sort különlegesnek hívjuk, ha bármely kék \(\displaystyle (k;j)\) esetén létezik \(\displaystyle l\), hogy \(\displaystyle (k;l)\) és \(\displaystyle (l;j)\) is piros. Bizonyítsuk be, hogy a színezgetés végeztével Ági talál különleges sort.
Javasolta: Paulovics Zoltán, Budapest
(5 pont)
A beküldési határidő 2025. március 10-én LEJÁRT.
Megoldás. A szimmetrikus színezési feltétel miatt – azaz hogy \(\displaystyle (i;j)\) és \(\displaystyle (j;i)\) közül pontosan az egyik piros – legfeljebb egy csupa piros sor létezik. A csupa piros sor nyilván különleges, hiszen nincs olyan (kék) mezője, melyre teljesülnie kellene a megadott feltételnek. Feltehető tehát, hogy nincs csupa piros sor.
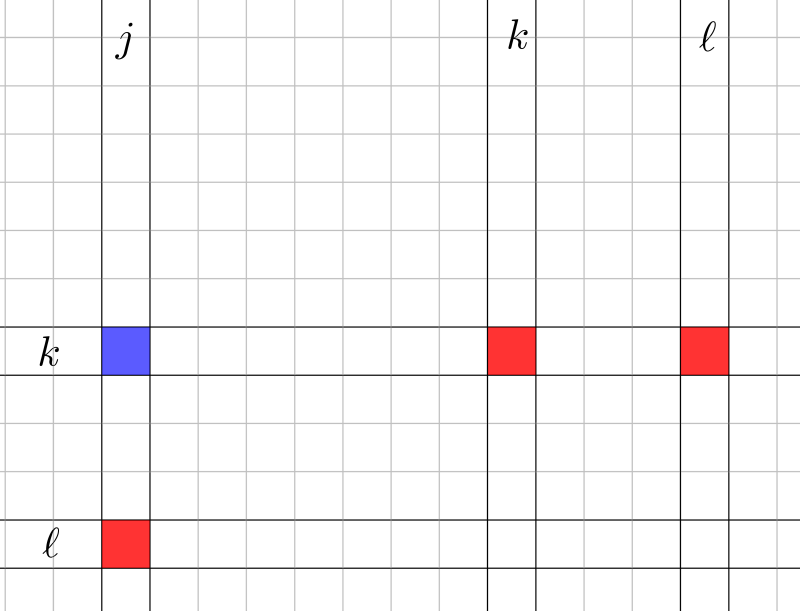
1. ábra. A különlegesség feltétele: bármely kék \(\displaystyle (k;j)\) esetén létezzen \(\displaystyle l\), hogy \(\displaystyle (k;l)\) és \(\displaystyle (l;j)\) is piros
Indirekt módon bizonyítunk: tegyük fel, hogy Ági nem talál különleges sort, azaz nincs olyan sor, amelyre bármely kék \(\displaystyle (k;j)\) mező esetén létezne \(\displaystyle l\), hogy a \(\displaystyle (k;l)\) és az \(\displaystyle (l;j)\) mezők is pirosak. Tehát bármely \(\displaystyle k\) sorra teljesül, hogy létezik olyan \(\displaystyle j\), melyre a \(\displaystyle (k;j)\) mező kék, és ha valamely \(\displaystyle l\)-re a \(\displaystyle (k;l)\) mező piros, úgy az \(\displaystyle (l;j)\) mező kék.
Ha viszont az \(\displaystyle (l;j)\) mező kék, úgy – a szimmetrikus színezési szabály miatt – a \(\displaystyle (j;l)\) mező piros. Azaz, ha a \(\displaystyle (k;l)\) mező piros, vagyis a \(\displaystyle k.\) sorban az \(\displaystyle l.\) oszlop piros, úgy a \(\displaystyle j.\) sorban is piros. Következésképpen a \(\displaystyle j.\) sorban legalább annyi piros van, mint a \(\displaystyle k.\) sorban. Sőt, több is, hiszen a \(\displaystyle (k;j)\) mező kék, míg a \(\displaystyle (j;k)\) mező piros. Az indirekt feltétel szerint nincs különleges sor, így tehát bármely sorhoz létezik olyan sor, amelyben több piros mező található, mint benne. Ez nyilvánvalóan ellentmondás.
Statisztika:
A C. 1844. feladat értékelése még nem fejeződött be.
A KöMaL 2025. februári matematika feladatai