 |
A C. 1851. feladat (2025. március) |
C. 1851. Egy háromszög \(\displaystyle C\) csúcsából induló belső szögfelező az \(\displaystyle AB\) oldalt a \(\displaystyle D\) pontban metszi. Mekkorák a háromszög oldalai, ha \(\displaystyle AD=15\), \(\displaystyle DB= 20\) és \(\displaystyle CD=f_{c}=12\sqrt{2}\)?
Javasolta: Németh László, Fonyód
(5 pont)
A beküldési határidő 2025. április 10-én LEJÁRT.
Megoldás. Tekintsük az alábbi ábrát, amelyen a feltételnek megfelelően \(\displaystyle c_1=15, c_2=20\) és \(\displaystyle f_c=12\sqrt{2}\).
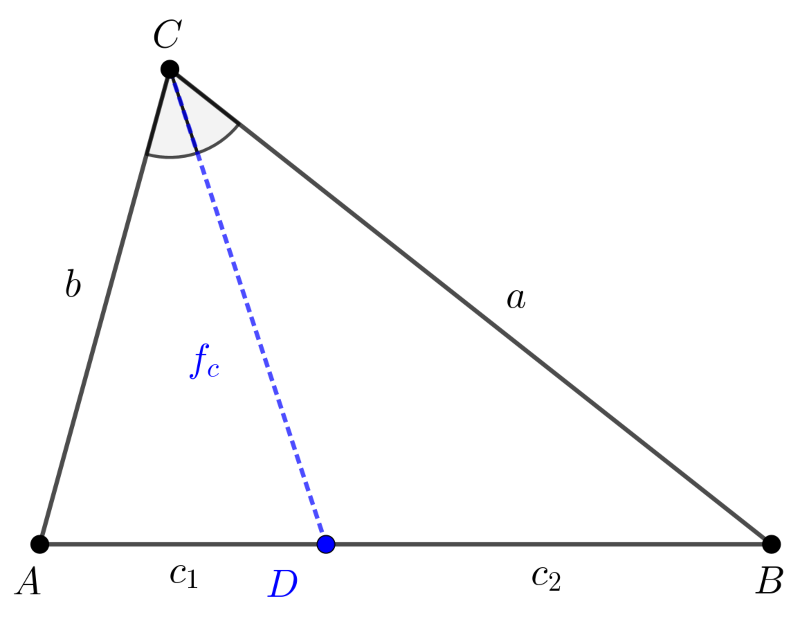
Felhasználjuk azt az ismert tételt, hogy a belső szögfelező négyzete a közrefogó oldalak szorzatának valamint azon két szakasz szorzatának a különbsége, amelyre a szögfelező a szemközti oldalt osztja (Geometriai feladatok gyűjteménye I., 1256.).
Eszerint \(\displaystyle f_c^2=a\cdot b-c_1\cdot c_2\), tehát a megadott értékekkel \(\displaystyle 288=a\cdot b-300\), ahonnan
| \(\displaystyle (1)\) | \(\displaystyle a\cdot b=588\) |
következik.
A belső szögfelezőtételből kapjuk, hogy \(\displaystyle \displaystyle{\frac{b}{a}=\frac{c_1}{c_2}}\), vagyis \(\displaystyle \displaystyle{\frac{b}{a}=\frac{15}{20}=\frac{3}{4}}\), ezért
| \(\displaystyle (2)\) | \(\displaystyle \displaystyle{b=\frac{3}{4}a}.\) |
A (2)-ben kapott eredményt (1)-be írva egyszerű számolás után kapjuk, hogy \(\displaystyle a^2=784\), ezért \(\displaystyle a=28\) és így (2) alapján \(\displaystyle b=21\).
A háromszög oldalai tehát
\(\displaystyle BC=a=28;\quad CA=b=21;\quad AB=c=35\)
egység hosszúságúak.
Statisztika:
37 dolgozat érkezett. 5 pontot kapott: Albert Luca Liliána, Balogh Péter, Bán Kincső Panni, Barna 201 Krisztina, Barsi Kíra Jázmin, Bencze Mátyás, Budai Máté, Farkas András, Farkas Máté, Hetyei Dániel, Illés Hanna, Iván Máté Domonkos, Kiss Máté, Kókai Ákos, Kriston Hunor, Kulcsár Anna Zita, Lukács Ármin, Masa Barnabás, Molnár Lili, Móricz Zsombor, Pánovics Máté, Pink István, Zhang Suan. 4 pontot kapott: Bernáth Csenge, Éliás Kristóf , Harmati Lőrinc Kenese, Jakab Dávid, Medgyesi Júlia, Nagy Nándor, Páternoszter Tamás, Rózsa Zsombor. 1 pontot kapott: 1 versenyző. Nem számítjuk a versenybe a születési dátum vagy a szülői nyilatkozat hiánya miatt: 1 dolgozat.
A KöMaL 2025. márciusi matematika feladatai