Középiskolai Matematikai és Fizikai Lapok
Informatika rovattal
Kiadja a MATFUND Alapítvány

Már regisztráltál?
Új vendég vagy?

A C. 803. feladat (2005. március)

C. 803. Oldjuk meg a következő egyenletrendszert:

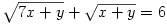
$\sqrt{7x+y}+\sqrt{x+y}=6$

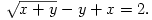
$\sqrt{x+y}-y+x=2.$

(5 pont)

A beküldési határidő 2005. április 15-én LEJÁRT.

Megoldás. Rendezzük az (1) egyenletet, majd emeljük négyzetre:

$\sqrt{7x+y} =6- \sqrt{x+y},$

$7x+y= 36- 12\sqrt{x+y}+ x+y.$

Innen $\sqrt{x+y}= \frac{6-x}{2}$ . A négyzetgyökvonás definíciója értelmében $\frac{6-x}{2}\ge 0$ , azaz x $\le$ 6. A $\sqrt{x+y}$ most kapott értékét helyettesítsük be a (2) egyenletbe:

$\frac{6-x}{2}- y+x=2.$

Innen x=2y-2. Helyettesítsünk (2)-be:

$\sqrt{2y-2+y}- y+2y-2=2.$

Rendezés és négyzetre emelés után a következő másodfokú egyenletet kapjuk:

y²-11y+18=0.

Ebből y₁=9 és x₁=16; vagy y₂=2 és x₂=2. A feltétel szerint x $\le$ 6, emiatt csak az x₂=2, y₂=2 lehet megoldása az egyenletnek. Helyettesítéssel könnyen ellenőrizhetjük, hogy ez valóban megoldás is.

Veres Gábor Pál (Miskolc, Földes Ferenc Gimn., 9. évf.)

Statisztika:

184 dolgozat érkezett.

5 pontot kapott: 145 versenyző.

4 pontot kapott: 8 versenyző.

3 pontot kapott: 7 versenyző.

2 pontot kapott: 4 versenyző.

1 pontot kapott: 8 versenyző.

0 pontot kapott: 7 versenyző.

Nem versenyszerű: 5 dolgozat.

A KöMaL 2005. márciusi matematika feladatai

184 dolgozat érkezett.
5 pontot kapott:	145 versenyző.
4 pontot kapott:	8 versenyző.
3 pontot kapott:	7 versenyző.
2 pontot kapott:	4 versenyző.
1 pontot kapott:	8 versenyző.
0 pontot kapott:	7 versenyző.
Nem versenyszerű:	5 dolgozat.