A C. 809. feladat (2005. április)

C. 809. Az egységnyi élű ABCDEFGH kocka AE élének felezőpontja P, a BCGF lap középpontja R.

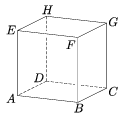
a) Mekkora területű síkidomban metszi a kockát a P, B, R pontokon átmenő sík?

b) A fenti sík két testre vágja a kockát. Mennyi a részek térfogatának az aránya?

(5 pont)

A beküldési határidő 2005. május 17-én LEJÁRT.

Megoldás. Jelölje I az EH él felezőpontját. Ekkor $IP \parallel GB$ , tehát a PBR pontokon átmenő sík megegyezik a PBGI pontokon átmenő síkkal.

a) A PBGI négyszög trapéz, $BG=\sqrt{1^2+1^2}=\sqrt2$ , $PI=BG/2={\sqrt2\over2}$ , $IG=PB=\sqrt{1^2+0,5^2}={\sqrt5\over2}$ . A trapéz magassága szintén a Pitagorasz-tétel segítségével számolható: $m=\sqrt{PB^2-((BG-PI)/2)^2}=\sqrt{18/16}=\sqrt2\cdot3/4$ . A trapéz területe ezek alapján:

$t={(\sqrt2+\sqrt2/2)\cdot\sqrt2\cdot3/4\over2}=9/8.$

b) BFGIEP csonkagúla. T_BFG=1/2, T_IEP=1/8, a magasság 1, így a csonkagúla térfogata:

$V={1\over3}\cdot\left({1\over2}+\sqrt{{1\over2}\cdot{1\over8}}+{1\over8}\right)={7\over24}.$

A másik rész térfogata $1-{7\over24}={17\over24}$ , így a két rész térfogatának aránya ${7\over17}$ .

Statisztika:

172 dolgozat érkezett.

5 pontot kapott: 99 versenyző.

4 pontot kapott: 21 versenyző.

3 pontot kapott: 24 versenyző.

2 pontot kapott: 13 versenyző.

0 pontot kapott: 11 versenyző.

Nem versenyszerű: 4 dolgozat.

A KöMaL 2005. áprilisi matematika feladatai

172 dolgozat érkezett.
5 pontot kapott:	99 versenyző.
4 pontot kapott:	21 versenyző.
3 pontot kapott:	24 versenyző.
2 pontot kapott:	13 versenyző.
0 pontot kapott:	11 versenyző.
Nem versenyszerű:	4 dolgozat.

Már regisztráltál?
Új vendég vagy?