Középiskolai Matematikai és Fizikai Lapok
Informatika rovattal
Kiadja a MATFUND Alapítvány
Már regisztráltál?
Új vendég vagy?

A C. 895. feladat (2007. április)

C. 895. A képen látható ábrasorozat egyre több sötét szabályos háromszögből készült. A látható szabálynak megfelelően elkészítjük az első n db ábrát. Hány sötét háromszöget használtunk fel összesen?

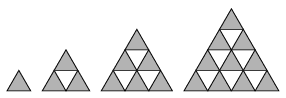
(5 pont)

A beküldési határidő 2007. május 15-én LEJÁRT.

Megoldás. A sötét háromszögek száma:

1+(1+2)+(1+2+3)+\cdots+(1+2+\cdots+n)=\frac{2\cdot1}{2}+ \frac{3\cdot2}{2}+\frac{4\cdot3}{2}+\cdots+\frac{(n+1)\cdot n}{2}=

=\frac{(1+1)1+(2+1)2+(3+1)3+\cdots+(n+1)n}{2}=\frac{(1^2+2^2+3^2+\cdots+n^2)+1\cdot(1+2+3+\cdots+n)}{2}=

=\frac{1}{2}\cdot\left(\frac{n(n+1)(2n+1)}{6}+\frac{(n+1)n}{2}\right)=\frac{n(n+1)(n+2)}{6}.

Statisztika:

211 dolgozat érkezett.
5 pontot kapott:118 versenyző.
4 pontot kapott:8 versenyző.
3 pontot kapott:8 versenyző.
2 pontot kapott:16 versenyző.
1 pontot kapott:26 versenyző.
0 pontot kapott:10 versenyző.
Nem versenyszerű:25 dolgozat.

A KöMaL 2007. áprilisi matematika feladatai