A G. 602. feladat (2017. május)

G. 602. Egy kútból kétféleképpen is fel lehet tölteni egy 3 m magas, kezdetben üres víztartályt. Egyszer úgy, hogy a \(\displaystyle \rm Cs_2\) csapon keresztül a víztartály aljára nyomjuk a vizet, a másik esetben pedig a víztartály tetején folyatjuk be a vizet a \(\displaystyle \rm Cs_1\) csapon keresztül.

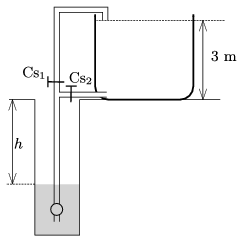
\(\displaystyle a)\) Melyik az olcsóbb megoldás?

\(\displaystyle b)\) Valaki kiszámította, hogy ha a szivattyú veszteségeit és a csőben áramló víz súrlódását elhanyagolhatjuk, akkor a tartály 20%-kal kevesebb energia felhasználásával is feltölthető, mint ha a gazdaságtalan megoldást választjuk. Milyen mélyen áll a víz a kútban? (A kút bővizű, a vízszint \(\displaystyle h\) mélysége a szivattyúzás során nem változik.)

Nagy László (1931–1987) feladata

(3 pont)

A beküldési határidő 2017. június 12-én LEJÁRT.

Megoldás. \(\displaystyle a)\) A víztartály megtöltése és az áramlások megszűnte után a víz mechanikai energiája (esetünkben a gravitációs helyzeti energiája) mindkét esetben ugyanakkorát változott. Ha azonban a Cs\(\displaystyle _1\) csapon keresztül töltjük fel a tartályt, a felülről lezúduló (átlagosan 1,5 méternyit eső) víz mozgási energiára is szert tesz, ami \(\displaystyle -\) az áramlások megszűnte után \(\displaystyle -\) a vizet melegíti, annak belső energiáját növeli. Emiatt a szivattyú munkavégzése (áram- vagy üzemanyagfogyasztása) ebben az esetben nagyobb lesz, ez a megoldás tehát drágább.

\(\displaystyle b)\) A végzett munka a víz tömegközéppontjának emelkedésével arányos. A megadott energiafelhasználási arány szerint

\(\displaystyle \frac{h+1{,}5~\rm m}{h+3{,}0~ \rm m}=0{,}8,\)

ahonnan a kérdezett vízmélység \(\displaystyle h=4{,}5~\rm m\).

A végzett munka kiszámításánál a magasságkülönbséget azért nem a szivattyú tényleges helyétől, hanem a kútban lévő víz felszínétől mértük, mert a helyzeti energia megváltozása szempontjából ez távolság a lényeges. A szivattyú ezt úgy ,,veszi észre'', hogy a fogyasztása a be- és kimeneti oldalon mérhető nyomások különbségével arányos. Ebből a különbségből kiesik a szivattyú tényleges helye, csak a vízszintek magasságkülönbsége jelenik meg a nyomáskülönbség képletében.

Statisztika:

20 dolgozat érkezett.
3 pontot kapott:	Bálint Boglárka Eszter, Békési Péter, Bonifert Balázs, Fekete András Albert, Fialovszky Márk, Földesi András, Geretovszky Anna, Horváth 999 Anikó, Kozmér Barbara, Pácsonyi Péter, Rusvai Miklós, Szakáll Lili, Tanner Norman, Vida Tamás.
2 pontot kapott:	Kozák 023 Áron, Urszuly Csenge.
1 pontot kapott:	3 versenyző.
0 pontot kapott:	1 versenyző.

A KöMaL 2017. májusi fizika feladatai