A G. 604. feladat (2017. május)

G. 604. Közepén ékkel alátámasztott, \(\displaystyle L=3\) m hosszú, vízszintes deszkán egy \(\displaystyle m_1=0{,}2\) kg tömegű és egy \(\displaystyle m_2=0{,}3\) kg tömegű, kis méretű test található. Közöttük egy \(\displaystyle \ell=0{,}3\) m-re összenyomott, fonállal rögzített, elhanyagolható tömegű, de erős rugó van. Az ék éppen a rendszer tömegközéppontja alatt van.

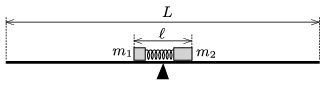
A fonalat elégetve az \(\displaystyle m_1\) tömegű testet \(\displaystyle v_1=2\) m/s sebességgel löki el a rugó. Melyik oldal felé és mennyi idő múlva billen meg a deszka? (A súrlódás elhanyagolható.)

Közli: Kobzos Ferenc, Dunaújváros

(3 pont)

A beküldési határidő 2017. június 12-én LEJÁRT.

Megoldás. A deszka tömegközéppontja is és a két kicsi test tömegközéppontja is az ék fölött van. Kezdetben az \(\displaystyle m_1\) tömegű test a deszka bal szélétől \(\displaystyle s_1=1{,}32\) m távol van, az \(\displaystyle m_2\) tömegű test a deszka jobb szélétől \(\displaystyle s_2=1{,}38\) m távol található.

A fonál elégetése után a rugó szétlöki a két testet, sebességük (a lendületmegmaradás törvénye szerint) \(\displaystyle v_1=2~\)m/s és \(\displaystyle v_2=1{,}33~\)m/s. Az erős rugó gyakorlatilag hosszának elhanyagolható megnövekedése után és igen rövid idő alatt löki szét a testeket. A szétlökött testek egyenletes mozgással közelednek a deszka végeihez, miközben a rendszer tömegközéppontja az ék fölött marad. A deszka csak akkor kezd el billenni, mikor valamelyik test eléri a deszka végét. Ez az \(\displaystyle m_1\) tömegű testtel történik meg előbb, a szétlökődéstől számított

\(\displaystyle t_1=\frac{s_1}{v_1}=0{,}66~\rm s\)

idő múlva. (A másik test csak 1,03 s alatt érné el a deszka szélét, ha a deszka nem billenne el már hamarabb.)

A deszka tehát kb. 0,7 másodperc múlva kezd el jobbra billenni.

Statisztika:

20 dolgozat érkezett.
3 pontot kapott:	Bálint Boglárka Eszter, Békési Péter, Fekete András Albert, Fialovszky Márk, Geretovszky Anna, Horváth 999 Anikó, Kozák 023 Áron, Kozmér Barbara, Merkl Levente, Pácsonyi Péter, Rusvai Miklós, Šárai Krisztina, Szakáll Lili, Urbán István, Vida Tamás.
2 pontot kapott:	Bonifert Balázs, Tanner Norman.
1 pontot kapott:	2 versenyző.
0 pontot kapott:	1 versenyző.

A KöMaL 2017. májusi fizika feladatai