A G. 619. feladat (2017. december)

G. 619. A kapcsolási rajzon szereplő hajlékony vezetékkel a \(\displaystyle C\) pontot vagy az \(\displaystyle X\), vagy az \(\displaystyle Y\) ponttal köthetjük össze.

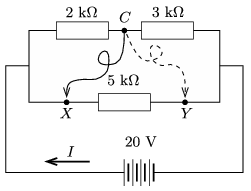
\(\displaystyle a)\) Mekkora ebben a két esetben a főág áramának \(\displaystyle I\) erőssége?

\(\displaystyle b)\) Mekkora ennek az áramnak az erőssége, ha a hajlékony vezetéket lekapcsoljuk a \(\displaystyle C\) pontról?

(3 pont)

A beküldési határidő 2018. január 10-én LEJÁRT.

Megoldás. \(\displaystyle a)\) Ha a vezetéket az \(\displaystyle X\) ponthoz kötjük, a 2 k\(\displaystyle \Omega\)-os ellenállást rövidre zárjuk, így az áramkör eredő ellenállása

\(\displaystyle R_X=\frac{3\cdot 5}{3+5}\,{\rm k}\Omega=1{,}875~{\rm k}\Omega,\)

a főág áramerőssége pedig

\(\displaystyle I_X=\frac{20~\rm V}{1{,}875\,{\rm k}\Omega}=10{,}7~\rm mA\)

lesz.

Hasonló módon számolva

\(\displaystyle R_Y=\frac{2\cdot 5}{2+5}\,{\rm k}\Omega=1{,}43~{\rm k}\Omega,\)

\(\displaystyle I_Y=\frac{20~\rm V}{1{,}43\,{\rm k}\Omega}=14{,}0~\rm mA.\)

\(\displaystyle b)\) Ha a hajlékony vezetéket lekapcsoljuk, az áramkör eredő ellenállása 2,5 k\(\displaystyle \Omega \), a főág áramerőssége pedig 8,0 mA lesz.

Statisztika:

47 dolgozat érkezett.
3 pontot kapott:	Baráth László, Barta Gergely, Bekes Barnabás, Bethlen Máté, Cseke Balázs, Csóti Balázs , Fekete Bálint Bertalan, Forgács Kata, Hartmann Alice, Huszár Anna, Jakó Attila György, Jánosik Máté, Kis-Bogdán Kolos, Kovács 062 Gábor, Kovács Kristóf, Láng Erik, Menyhárt Tamás, Nagy Zalán, Papp Viktória, Rácz Tamás Gáspár, Sebestyén Pál Botond, Szakáll Lili, Szántó Barnabás, Tanner Norman, Toronyi András, Viczián András.
2 pontot kapott:	Andó Lujza, Egyed Márton, Köpenczei Csanád.
1 pontot kapott:	15 versenyző.
0 pontot kapott:	3 versenyző.

A KöMaL 2017. decemberi fizika feladatai