 |
A G. 651. feladat (2018. november) |
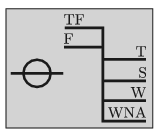
G. 651. Az óceánjáró hajók oldalán látható az úgynevezett Plimsoll-jel. Ez megmutatja, hogy milyen mélyen merül be a vízbe a hajó a különböző vizekben, ha a megengedett maximális tömegű rakománnyal terhelik. (TF = Tropical Fresh Water; F = Fresh Water; T = Tropical Seawater; S = Summer Seawater; W = Winter Seawater; WNA = Winter North Atlantic.)
A legfelső, TF jelű vonal a trópusi édesvíz (sűrűsége 996 kg/m\(\displaystyle {}^3\)) esetén érvényes bemerülést jelzi, alatta a mérsékelt övi édesvíz (sűrűsége 999 kg/m\(\displaystyle {}^3\)) esetén érvényes, F jelű vonal látható. Egy bizonyos hajón a két vonal távolsága 7 cm. Mekkora a téli tengervíz sűrűsége, ha a W feliratú, a téli tengervízben érvényes vonal a legfelső vonaltól 21 cm-rel lejjebb van?
(4 pont)
A beküldési határidő 2018. december 10-én LEJÁRT.
Megoldás. A különböző hőmérsékletű és sótartalmú tengervizek sűrűsége csak kicsit különbözik egymástól, és a hajó keresztmetszete sem változik lényegesen, ha a bemerülési mélység 10-20 cm-rel változik. Emiatt a bemerülési mélység változása – jó közelítéssel – a sűrűségkülönbségekkel arányos. Ha a legfelső 2 vonal távolsága 7 cm, és ez 3 kg/m\(\displaystyle ^3\) sűrűségváltozásnak felel meg, akkor a 21 cm-es vonaltávolsághoz 9 kg/m\(\displaystyle ^3\) tartozik. A W jelű téli tengervíz sűrűsége tehát (996+9) kg/m\(\displaystyle ^3 \)=1005 kg/m\(\displaystyle ^3\).
Megjegyzés. Ha pontosabban számolunk, akkor a kérdéses sűrűségre (kg/m\(\displaystyle ^3\) egységekben számolva) az
\(\displaystyle \frac{1-\frac{996}{999} }{1-\frac{996}{\varrho} }=\frac{7}{21}\)
egyenletet írhatjuk fel, ahonnan \(\displaystyle \varrho=1005,055~\rm kg/m^3\) adódik. Ilyen pontosságú számolás azonban indokolatlan, hiszen a megadott 7 cm-es és 21 cm-es adat kiírt számjegyeinek száma arra utal, hogy ezeket a távolságokat is csak néhány százalékos pontossággal ismerjük.
Statisztika:
A KöMaL 2018. novemberi fizika feladatai