 |
A G. 662. feladat (2019. február) |
G. 662. Az (a) és a (b) ábrán látható összeállítás egy nagyobb korongból és egy-egy, hozzá koncentrikusan rögzített, kisebb hengerből áll. A kis hengerekre fonalakat csévéltünk, amelyeknek végét egy rúd segítségével vízszintesen, v sebességgel mozgatjuk.
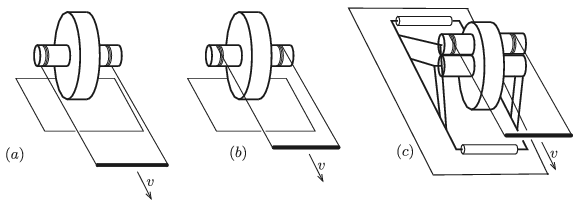
A (c) esetben a kis hengerhez felülről egy vele azonos átmérőjű, szabadon forgó másik kis henger is csatlakozik. A felső henger nekiszorul az alsónak, és a lebillenését egy-egy görgőhöz csatlakozó rúdszerkezet akadályozza meg. A felső hengerre is fonalat csévéltünk, és a fonál végét v sebességgel húzzuk. A korongok a talajon, illetve a kis hengerek egymáson nem csúsznak meg.
Melyik irányban, és v-nél nagyobb vagy kisebb sebességgel fog mozogni a korong középpontja az egyes esetekben?
(3 pont)
A beküldési határidő 2019. március 11-én LEJÁRT.
Megoldás. Mindhárom esetben a korong középpontja ugyanolyan irányban (előrefelé) mozog, mint amerre a fonalakat húzzuk. Az (a) és a (c) esetben a korong v-nél nagyobb sebességgel, a (b) esetben pedig v-nél kisebb sebességgel gördül előre a korong.
Megjegyzés. Ha a korong sugara R, a kis hengereké pedig r, akkor a korong középpontjának sebessége a három esetben:
ua=uc=RR−rv,ub=RR+rv.
Ezeket az összefüggéseket (amelyek levezetése nem tartozik a feladathoz) legkönnyebben a korong középpontjával együtt mozgó koordináta-rendszerben lehet megkapni. Ebből a rendszerből nézve a korong középpontja áll (tehát a korong csak forog), a fonál v−u sebességgel halad előrefelé, a talaj pedig u sebességgel hátrafelé. Ezek a sebességek a rögzítettnek tekinthető forgástengelytől mért távolsággal arányosak:
v−uaua=−rR;v−ubub=+rR;uc−vuc=+rR.
Statisztika:
27 dolgozat érkezett. 3 pontot kapott: Sárvári Borka Luca. 2 pontot kapott: Bánáti Tamás, Koczkás József Dániel, Kovács Alex, Markó Péter , Sebestyén József Tas, Somlán Gellért, Szántó Barnabás, Szőllősi Gergely, Téglás Panna, Török 111 László. 1 pontot kapott: 6 versenyző. 0 pontot kapott: 10 versenyző.
A KöMaL 2019. februári fizika feladatai
|
|

