A G. 715. feladat (2020. szeptember)

G. 715. Egy áramkör három ellenállásból és egy telepből áll az ábrán látható módon.

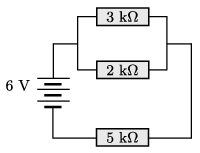
\(\displaystyle a)\) Mekkora az egyes ellenállásokon átfolyó áram és a rajtuk eső feszültség?

\(\displaystyle b)\) Hogyan változnak ezek az értékek, ha a két párhuzamos ellenállás mellé még bekötünk rengeteg (,,végtelen sok'') \(\displaystyle 1~\mathrm{k}\Omega\)-os ellenállást párhuzamosan?

\(\displaystyle c)\) Mekkora lesz az eredeti áramkör három ellenállásának árama és feszültsége, ha az \(\displaystyle 5~\mathrm{k}\Omega\)-os ellenállás mellé bekötünk még rengeteg (,,végtelen sok'') \(\displaystyle 1~\mathrm{k}\Omega\)-os ellenállást sorosan?

(A nyomtatásban megjelent feladat ábráján tévesen szerepelnek az ellenállások. Helyesen mindhárom ellenállás nagysága k\(\displaystyle \Omega\)-ként értendő.)

(4 pont)

A beküldési határidő 2020. október 15-én LEJÁRT.

Megoldás. \(\displaystyle a)\) Jelöljük az egyes ellenállásokra eső feszültségeket és áramerősségeket az ellenállás nagyságának megfelelő indexekkel. A teljes áramkör eredő ellenállása

\(\displaystyle R_\text{eredő}=\left(\frac{2\cdot 3}{2+3}+5\right){\rm k\Omega}=\frac{31}{5}\,{\rm k\Omega}=6{,}2~{\rm k\Omega}.\)

Eszerint

\(\displaystyle I_5=\frac{6~\rm V}{6{,}2~{\rm k\Omega}}=\frac{30}{31}~{\rm mA}\approx 0{,}97~ {\rm mA} \qquad \text{és} \qquad U_5=5~{\rm k\Omega}\cdot\frac{30}{31}~{\rm mA}\approx 4{,}84~{\rm V}.\)

A párhuzamosan kapcsolt ellenállásokra

\(\displaystyle U_2=U_3=6~{\rm V}-U_5=\frac{36}{31}~{\rm {V}}\approx 1{,}16~\rm V\)

feszültség jut, és a rajtuk árfolyó áram erőssége

\(\displaystyle I_2=\frac{U_2}{2~{\rm k\Omega}}=\frac{18}{31}\,{\rm mA}\approx 0{,}58~{\rm mA},\)

illetve

\(\displaystyle I_3=\frac{U_3}{3~{\rm k\Omega}}=\frac{12}{31}\,{\rm mA}\approx 0{,}39~{\rm mA}.\)

\(\displaystyle b)\) A nagyon sok párhuzamosan kapcsolt ellenállás eredője gyakorlatilag nulla, tehát ezek rövidre zárják az áramkör felső részét. Ennek megfelelően

\(\displaystyle U_2=U_3=0,\qquad I_2=I_3=0,\)

továbbá

\(\displaystyle U_5=6~{\rm V}\qquad \text{és} \qquad I_5=1{,}2~\rm mA.\)

\(\displaystyle c)\) A nagyon sok sorosan kapcsolt ellenállás gyakorlatilag megszakítja az áramkört, tehát

\(\displaystyle I_2=I_3=I_5=0 \qquad \text{és}\qquad U_2=U_3=U_5=0.\)

Statisztika:

59 dolgozat érkezett.
4 pontot kapott:	Bacsó Dániel, Bencz Benedek, Biszak Ákos, Cynolter Dorottya, Czirók Tamás, Jeney Zsolt, Josepovits Gábor, Kohut Márk Balázs, Kovács Dorina , Lőrincz Gergely, Marozsi Lenke Sára, Milassin Brúnó, Molnár Kristóf, Móricz Benjámin, Richlik Márton, Salamon Zsigmond, Sebestyén József Tas, Szabó Márton, Szanyi Attila, Tarján Bernát, Vágó Botond, Veszprémi Rebeka Barbara, Vincze Farkas Csongor.
3 pontot kapott:	Bartók Vince, Bruder László, Fehérvári Donát, Ignácz Patrik , Jeszenői Sára, Láng Erik, Patricia Janecsko, Rózsa Félix, Schneider Dávid, Szabó Réka, Szeibert Dominik, Töreczki Gábor.
2 pontot kapott:	11 versenyző.
1 pontot kapott:	5 versenyző.
0 pontot kapott:	6 versenyző.
Nem versenyszerű:	1 dolgozat.
Nem számítjuk a versenybe a születési dátum vagy a szülői nyilatkozat hiánya miatt:	1 dolgozat.

A KöMaL 2020. szeptemberi fizika feladatai