 |
A G. 728. feladat (2020. december) |
G. 728. Vannak olyan folyadékok, például a nyers tej vagy az olívaolajos-balzsamecetes salátaöntet, melyeket ha állni hagyunk, akkor a folyadék két alkotóelemére válik szét. Az olaj kerül az öntet tetejére, illetve zsíros tejszín lesz a tej tetején, miközben a teljes térfogat nem változik. Ha az ilyen folyadékokat
\(\displaystyle a)\) felfelé keskenyedő üvegben tartjuk;
\(\displaystyle b)\) hengeres mérőpohárba töltjük;
\(\displaystyle c)\) felfelé szélesedő pohárba öntjük,
majd megvárjuk az alkotóelemek szétválását, akkor a folyadék aljánál a hidrosztatikai nyomás megnő, lecsökken vagy változatlan marad?
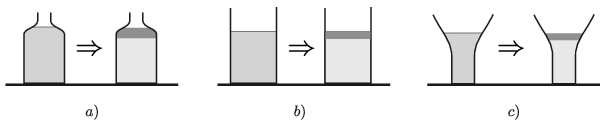
(4 pont)
A beküldési határidő 2021. január 15-én LEJÁRT.
I. megoldás. Tekintsünk egy olyan – az edény közepénél elhelyezkedő – folyadékoszlopot, amely nem érintkezik az edény falával. Ennek az oszlopnak sem a magassága, sem az alapterületének keresztmetszete nem változik, így az általa kifejtett nyomás az átlagsűrűségével arányosan változik, vagy marad változatlan.
\(\displaystyle b)\) A mérőpohár esetében a folyadékoszlop átlagsűrűsége ugyanannyi, mint a folyadék egészének átlagsűrűsége, az viszont nyilván nem változik, mert a folyadék össztömege is és a térfogata változatlan marad. Ekkor tehát az edény aljánál az alkotórészek szétválása során a folyadék nyomása nem változik.
\(\displaystyle a)\) A felfelé keskenyedő üvegben a kisebb sűrűségű rész (az olaj, illetve a tejszín) kisebb keresztmetszetű részbe szorul, tehát a kiválasztott hengeres részben az átlagsűrűség lecsökken, és így a folyadék nyomása az edény aljánál lecsökken.
\(\displaystyle c)\) A felfelé szélesedő edényben a kisebb sűrűségű összetevő a folyadék felső részénél szétterül, emiatt a vizsgált hengeres rész átlagsűrűsége megnő, és vele együtt a folyadék aljánál a nyomás is megnő.
II. megoldás. Az edény alá helyezett mérleg a folyadék és az edény teljes \(\displaystyle G\) súlyát mutatja; ez a komponensek szétválása során nyilván nem változik.
A folyadék által az edény aljára kifejtett, a folyadék ottani nyomásával arányos \(\displaystyle F\) erő (ennek esetleges változását kérdezi a feladat) nem egyezik meg a folyadék \(\displaystyle G_\text{folyadék}\) súlyával, annál nagyobb vagy kisebb is lehet.
Az edény falának egyensúlyát kifejező egyenlet:
\(\displaystyle G_\text{edény}+F-F_\text{fal}-G=0,\)
ahol \(\displaystyle F_\text{fal}\) a folyadék felső része által az edény falára kifejtett függőleges irányú eredő erő. (Ez utóbbit felfelé mutató irányban tekintjük pozitívnak.)
A fenti egyenletből
\(\displaystyle F=G-G_\text{edény}+F_\text{fal}.\)
Mivel \(\displaystyle G=G_\text{edény}+G_\text{folyadék}\), továbbá a folyadék súlyának és az edény súlyának változatlansága miatt a fenti egyenlet írható:
\(\displaystyle F=G_\text{folyadék}+F_\text{fal}=\text{állandó}+F_\text{fal}.\)
\(\displaystyle a)\) A felül összeszűkülő edényben a folyadék felső részének sűrűsége lecsökken, így a folyadék kevésbé nyomja felfelé az edényt, tehát a kérdezett nyomás is lecsökken.
\(\displaystyle b)\) Hengeres mérőpohárban \(\displaystyle F_\text{fal}=0\), tehát az alkotóelemek szétválása során a fenéknyomás nem változik.
\(\displaystyle c)\) A felfelé szélesedő edényben a folyadék felső része lefelé nyomja az edényt, tehát \(\displaystyle F_\text{fal}<0\). A komponensek szétválása során a felső folyadékrész sűrűsége csökken, tehát \(\displaystyle \vert F_\text{fal}\vert\) is csökken,
\(\displaystyle F_\text{fal}=-\vert F_\text{fal}\vert,\)
tehát az edény aljánál fellépő nyomás növekszik.
Statisztika:
35 dolgozat érkezett. 4 pontot kapott: Beke Botond, Bencz Benedek, Czirók Tamás, Láng Erik, Marozsi Lenke Sára, Mázsi Áron, Patricia Janecsko, Sebestyén József Tas, Szegedi Ágoston, Szitka Virág, Telkes Ágota, Vágó Botond, Vincze Farkas Csongor, Vízi Zalán, Waldhauser Miklós. 3 pontot kapott: Dancsák Dénes, Molnár Kristóf. 2 pontot kapott: 5 versenyző. 1 pontot kapott: 5 versenyző. 0 pontot kapott: 6 versenyző. Nem versenyszerű: 2 dolgozat.
A KöMaL 2020. decemberi fizika feladatai