 |
A G. 735. feladat (2021. február) |
G. 735. Az ábrán látható hengerkerék szabadon foroghat egy rögzített tengely körül. A mozgócsigák tömege m1 és m2 (m1<m2). Milyen irányban és mekkora erővel kell húznunk a bal oldali legszélső kötélszálat, hogy a rendszer egyensúlyban legyen? (A kötél nem csúszik meg a csigákon.)
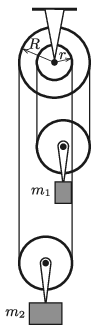
Adatok: R=10 cm, r=5 cm, m1=2 kg, m2=3 kg.
Közli: Holics László, Budapest
(4 pont)
A beküldési határidő 2021. március 16-án LEJÁRT.
Megoldás. A kötelet felfelé kell húznunk F=R−r2R(m2−m1)g≈2,5 N nagyságú erővel.
Statisztika:
30 dolgozat érkezett. 4 pontot kapott: Bencz Benedek, Buzási-Temesi Imre, Cynolter Dorottya, Hegedűs Máté Miklós, Hudvágner Márton, Jeszenői Sára, Josepovits Gábor, Kohut Márk Balázs, Kovács Dorina , Marozsi Lenke Sára, Molnár Kristóf, Novák Péter, Patricia Janecsko, Sebestyén József Tas, Szabó Réka, Vágó Botond, Veszprémi Rebeka Barbara, Vig Zsófia, Vincze Farkas Csongor, Waldhauser Miklós, Wórum Soma. 3 pontot kapott: Beke Botond, Bogdán Benedek, Czirók Tamás, Lipóczi Levente, Richlik Márton. 2 pontot kapott: 4 versenyző.
A KöMaL 2021. februári fizika feladatai
|
|

