A G. 759. feladat (2021. november)

G. 759. Egy vízszintes, súrlódásmentes, rögzített pálcára felfűzve négy darab $\displaystyle m$ tömegű, négy darab $\displaystyle M$ tömegű $\displaystyle (m<M)$, majd ismét egy $\displaystyle m$ tömegű, tökéletesen rugalmas golyó áll közel egymáshoz az ábrán látható elrendezésben. Balról egy $\displaystyle m$ tömegű, szintén tökéletesen rugalmas golyó érkezik $\displaystyle v$ sebességgel, és ütközik a golyósor első tagjával.

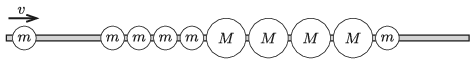
A további ütközések lezajlása után mely golyók maradnak nyugalomban, és a többiek milyen irányban fognak mozogni?

(4 pont)

A beküldési határidő 2021. december 15-én LEJÁRT.

Megoldás: Ha egy álló, A jelű testnek tökéletesen rugalmasan nekiütközik egy másik (B jelű) test $\displaystyle v$ sebességgel, akkor a tömegüktől függően háromféle eset valósulhat meg:

$\displaystyle (i)$ Ha $\displaystyle m_A=m_B$, akkor $\displaystyle B$ megáll, A pedig $\displaystyle v$ sebességgel indul el.

$\displaystyle (ii)$ Ha $\displaystyle m_A>m_B$, akkor a B test $\displaystyle v$-nél kisebb sebességgel visszapattan, A pedig ugyancsak $\displaystyle v$-nél kisebb sebességgel indul el ,,előre''.

$\displaystyle (iii)$ Ha $\displaystyle m_A<m_B$, akkor a B test $\displaystyle v$-nél kisebb $\displaystyle v_1$ sebességgel előrefelé mozog tovább, A pedig $\displaystyle v_1$-nél nagyobb sebességgel indul el előre.

(Az ,,előre'' és ,,hátra'' irányokat az álló testnek ütköző másik test korábbi sebességéhez viszonyítjuk.)

Számozzuk meg a 10 testet balról jobbra növekvő számokkal 1-től 10-ig. A sorozatos ütközések így zajlanak le:

– Az 1. test megáll, a 2. elindul $\displaystyle v$ sebességgel.

– A 2. test megáll, a 3. elindul $\displaystyle v$ sebességgel.

– A 3. test megáll, a 4. elindul $\displaystyle v$ sebességgel.

– A 4. test megáll, az 5. elindul $\displaystyle v$ sebességgel.

– Az $\displaystyle m$ tömegű 5. test ütközik a nála nagyobb tömegű 6. testtel. Az ütközés után az 5. test balra mozog $\displaystyle v_1<v$ sebességgel, a 6. pedig jobbra $\displaystyle v_2<v$ sebességgel.

– Az $\displaystyle m$ tömegű testek sorozatos ütközése után az 1. test végül balra fog mozogni $\displaystyle v_1<v$ sebességgel, a 2., 3., 4., és 5. test pedig megáll.

– Az $\displaystyle M$ tömegű testek sorozatos ütközése után a 6., 7., 8., megáll, a 9. pedig $\displaystyle v_2$ sebességgel nekiütközik a 10. testnek.

– Az ütközés után a 9. test jobbra fog mozogni $\displaystyle v_3<v_2$ sebességgel, a 10. pedig ugyancsak jobbra $\displaystyle v_4 > v_3$ sebességgel.

Összefoglalva: az ütközéssorozat végén a bal szélső test balra, a jobb szélső két test pedig jobbra fog mozogni, a többi pedig nyugalomban marad.

Megjegyzés. Az energia- és a lendületmegmaradás törvényét alkalmazva kiszámíthatjuk, hogy

$\displaystyle v_1=\frac{M-m}{M+m}v, \qquad v_3=\frac{2m(M-m)}{(M+m)^2}v \qquad \text{és}\qquad v_4=\frac{4Mm}{(M+m)^2}v.$

Statisztika:

34 dolgozat érkezett.
4 pontot kapott:	Beke Botond, Csilling Dániel, Fehérvári Donát, Glaser Dávid, Hruby Laura, Jávor Botond, Kiss 668 Benedek, Klement Tamás, Kovács Klára, Marosi Botond Máté, Nagy 333 Zalán, Sütő Áron, Téglás Dorka, Török Hanga.
3 pontot kapott:	Cserényi Bendegúz, Sós Ádám.
1 pontot kapott:	7 versenyző.
0 pontot kapott:	7 versenyző.
Nem versenyszerű:	1 dolgozat.

A KöMaL 2021. novemberi fizika feladatai